第11回 凸関数 [ネコ騙し数学]
第１１回 凸関数
いよいよ微分のハイライト、凸関数ですにゃ。
「これを語らずして、何のための微分！！」ですにゃ。
ネムネコ、いつにも増して力を入れて説明しますにゃ。
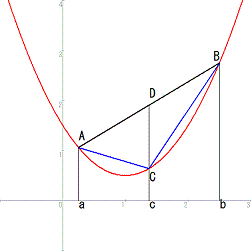
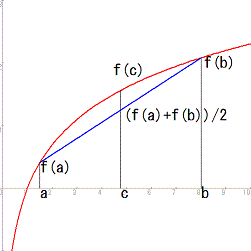
y＝ｆ(x)上にある任意の二点A(a,f(a))とB(b,f(b))の間において、弦ABが線分ABよりも下側にある関数を凸関数といいますにゃ。
図を見るとわかりますが、a < c < b の時、
線分ACの傾き≦線分ABの傾き≦線分CBの傾き
という関係がありますにゃ。
式で書くと、
という関係がありますにゃ。
「おい、バカ猫。これは証明しなくていいんか？」
「まるでネムネコのようにうるさい野郎だ。DはCの上側にあるから、AB（AD）の傾きはACの傾きより小さくないだろう。で、CはDの下側にあるから、CBの傾きはAC（DB）の傾きより小さくないんだよ。」
「それはそれとして、俺にはこの関数は凹に見えるが、何で凸なんだ？呼ぶんなら凹関数だろう？」
「そんなの知らねぇよ。そう呼ぶんだから、しょうがないだろう。俺に聞くな！！」
ちなみに、弦ABが線分ABの上側にある関数を「下に凸」と呼んだりしますにゃ。
逆、つまり、a < c < bで
が成り立つとき、
fは凸関数になりますにゃ。
凸関数の条件を
としてもいいですにゃ。同じことですから。
ここまでは一般論です。
では、微分可能な関数の場合、これがどうなるかと言いますと、『解析概論』の定理２５を引用しますと、
定理 ｆ''(x)が存在する場合には、
（１）区間内で常に
ならば、f(x)は凸関数である。
（２）ｆ(x)が凸関数であるならば、区間内で常に
にゃ。
ここで、
f''(x)はy＝f(x)を二回微分した関数にゃ。
たとえば、
とすると、これを一回ｘで微分すると
だにゃ。これをもう一回ｘで微分すると、
となるにゃ。
で、微分の公式
を使っていますにゃ。
よもやと思うけろ、この公式、忘れてないけろな？
（１）の証明には、「平均値の定理」を使うにゃ。
②の式の左辺に平均値の定理を使うと
右辺に平均値の定理を使うと
になりますにゃ。
常に、
ということは、「f'(x)が単調に増加している」ということだから、
より
となって、
になるにゃ。
これで（１）の証明は終わりにゃ。
（２）の証明は、是非、チャレンジして欲しいにゃ(^^♪
ここで、大切なのは、
「ならば凸関数で、凸関数ならば」
ということにゃ。
そして、
「
ならば下に凸で、下に凸なら」
ということにゃ。
さらに、二回、微分可能で凸関数ならば、
y＝ｆ(x)の曲線は、その曲線上の接線よりも上側にある
という性質があります。
接点のｘ座標をaとすると、接線の方程式は
ですので、証明すべきものは
ですね。
証明は意外に簡単で、
で、前回、
「f(x)－f(a)のような関数の差の形では、ｆが微分可能なら、平均値の定理が使える」
と言いましたが、これを使うと
平均値の定理から
となって、このcはｘとaの間に存在する。これを③式に代入すると、
となります。
ならば、f'(x)は増加関数。
ｘ＜aの時はcはｘとaの間にあるのだから
となって、
また、a ≦xならばa < c <xで
が成立する。
丁寧に書きましたから長くなりましたけれども・・・。
逆に
、つまり、「下に凸の関数」の場合、曲線の接線はかならず曲線の上の位置に存在する。
前回の
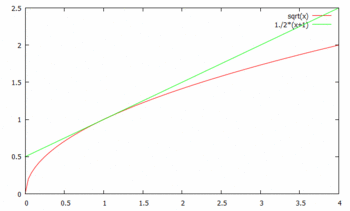
これなんかは「下に凸の関数」で、接線は曲線の上に位置しているでしょ。
ですから、微分の公式
（この式、忘れてねえよな？）
を使うと、この微分は
となり、
ですから、y'' < 0となって下に凸の関数。
では、
はどうでしょう？
この関数の定義域は－∞ < x < ∞、つまり実数全域とします。
この二階微分ｙ’’は
となるので、x < 0では負で「下に凸」、x ≧ 0 では０以上となるので「上に凸」であることが分かります。そして、x＝0で「下に凸」が「上に凸」に変わっている。このような点を変曲点といいますにゃ。
ちなみに、
や
のような関数の二階微分はなのでx＝0の前後でf''(x)がマイナスになったりしないので、ｘ＝０は変曲点ではありません。
で、のグラフ。
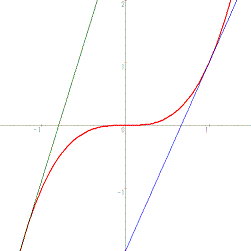
x＝1とx＝－1.5の時の接線も合わせて書きました。
この図から、接線と曲線の上下関係が逆転していることも分かるんじゃないでしょうか。
上の図は
のグラフです。微分積分で扱う対数関数logは自然底e＝2.71828…の対数関数で10を底にするもの
とは違いますにゃ。
その内にこの関数の微分をやりますけれども、
です。ですから、
となってこの関数は下に凸の関数ですにゃ。
対数関数の微分を知らなくても、図を見れば、対数関数が下に凸であることは明らか！！
で、
ですにゃ。
この図を見ると、
が
の上になりますにゃ。
つまり、
対数関数は増加関数だから、
凸関数（正確には「下に凸」）の性質を使うことで、相加平均≧相乗平均ができたにゃん。
スゴイにゃん。
そして、これを少し工夫すれば、
も証明できる。
これだけではなく、0≦x≦πではsinxは上に凸、cosxは下に凸だから、
という不等式が出て来るにゃ。
―――sin、cosの微分を知らないなんて言ってはいけない。グラフを書けば、上に凸か、下に凸かはすぐに分かる！！―――
ちなみに、
だから、
にゃ。
√xは上に凸だから、
にゃ。そして、こんな不等式まで出て来るにゃ。
なお、a≧0、b≧0、そして、
です。
この不等式は、√を対数logに変えても、成立しますよ。
どちらも「下に凸の関数」だからです。
そして、「上に凸の関数」ならば、「≧」の向きが「≦」に変わります。
タグ：微分積分
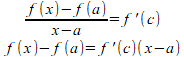
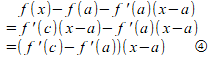
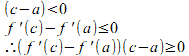
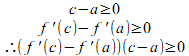
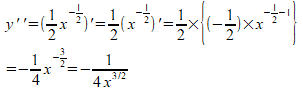
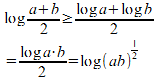
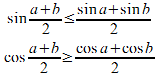
この段階で初歩の質問です。
二階微分というのは 一階微分と同じにしかならないように感じるのですが。
つまり 一階微分は すでにもう斜めであっても直線になっているのではないかと。
なぜ二階も三階も微分できるのですか？
by bragelone (2015-03-03 12:01)
ダイセルリサーチセンターの久保田邦親博士（工学）材料物理数学再武装は面白いですよ。マルテンサイトの強度と靭性のバランスが科学的に求まるのは品質工学をやっていてありがたい。
by マリンエンジニア (2021-03-03 18:38)
あれね。非線形回帰の本質的問題点をついているよね。いろんな
な回帰計算があり、人工知能がなぜシグモイド関数を基底関数と
しているのかの説明。フーリエとテイラーとかあるけれどどれも
基底関数の多項式近似回帰なんだけど、例えば２つの関数の特徴を
合成したいばあいその２つの関数と似ても似つかなくなる。シグモイド関数をつかって合成するともとの関数が保存された形式で式が簡単にできると関数接合論はいっている。
by ダイヤモンド富士 (2022-04-26 03:38)
コペルニクス的転回だな。なにやら教育関係者なんかでも話題になっているらしい。
by DXイノベーションネットワーク (2022-06-03 02:00)
本当だ経済学の祖アダムスミスの神の見えざる手が計算できた。
by CAE (2022-06-03 19:43)
CAE解析で使われているマトリックス（行列式）計算って昔アラブのえらいお坊さんが考え出したってしってる？なんかコーヒルンパみたいなはなしがイスラム数がなんだ。
by 安来キツネダンス (2023-03-14 00:43)
博士は元プロテリアル（旧日立金属）で有名な特殊鋼合金SLD-MAGICを発明された方なんですね。なんだかわからないけど下町ロケットの佃製作所みたいな話がFacebookにありました。
by グリーンモノづくり (2023-10-28 00:35)
名門の輝き日本刀の刃先にできるマルテンサイトはロケットの切り離しの刃にも使われているのをどこかで読みました。それにしても、材料物理数学再武装の関数接合論、ビジネスー経営工学関係ではKPI競合モデルと呼ばれ博士は別名炎の経営者なんて暗号名のような呼ばれ方もしているようだ。
by 熱処理関係 (2023-12-28 10:52)