第42回 ルンゲ=クッタ法で二階微分方程式を解く [ネコ騙し数学]
第42回 ルンゲ=クッタ法で二階微分方程式の初期値問題を解く
二階の常微分方程式の一般形は
と書けますにゃ。
ここで、
ですにゃ。
で、
とすると、①は
という一階の連立微分方程式に変換できるんだにゃ。
すると、ルンゲ=クッタ法を使って、この微分方程式の初期値問題を数値的に解くことができるケロ。
計算法は、
まず、
と値を更新し、
また最初から計算しなおすというシンプルなもの。
こんな簡単なもので、
二階微分方程式の初期値問題は、ほとんどすべて、高精度の数値解を求められるってんだから、驚きだにゃ。
十進BASICのプログラムは、
SET WINDOW -1,10,-2,2
DRAW axes
REM dp/dt = f(x,y,p)の設定
DEF f(x,y,p) = -y
REM h:xの増分
LET h = 0.1
LET n = 100
REM 初期値の設定
LET x0 = 0
LET y0 = 0
LET p0 = 1.0
rem
REM ルンゲ=クッタ法のメインの計算
LET x = x0
LET y = y0
LET p = p0
PLOT LINES:x,y;
FOR i = 1 TO n
LET dp1 = h*f(x,y,p)
LET dy1 = h*(p)
LET dp2 = h*f(x+h/2,y+dy1/2,p+dp1/2)
LET dy2 = h*(p+dp1/2)
LET dp3 = h*f(x+h/2,y+dy2/2,p+dp2/2)
LET dy3 = h*(p+dp2/2)
LET dp4 = h*f(x+h,y+dy3,p+dp3)
LET dy4 = h*(p+dp3)
LET x = x+h
LET p = p + (dp1+2*dp2+2*dp3+dp4)/6
LET y = y + (dy1+2*dy2+2*dy3+dy4)/6
PLOT LINES:x,y;
NEXT i
END
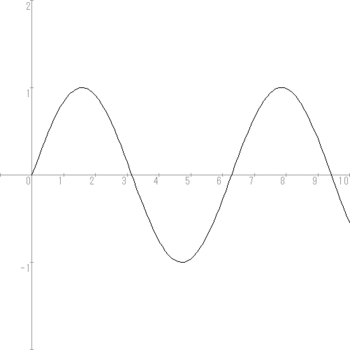
このプログラムで解いているのは、
y'' = – y
という微分方程式で、
初期条件としてx = 0のとき、y = 0, y' = 0を与えているにゃ。
この解は y = sinx、 p = dy/dt = cosxなんだけれど、解いた結果は次のとおり。
綺麗な正弦曲線になっていて、周期も2πになっていることがわかるケロ。
でも、ネムネコがやりたいのは、これじゃ~ない。
理系の人や高校で物理を習った人は、振り子の運動方程式が
なることを習ったはずにゃ。で、θ ≪ 1ならば、sinθ ≒ θ と近似できるから、
となり、単振動になる。その周期Tは
となると習ったはずにゃ。
これを、ルンゲ=クッタ法で正確に解こうじゃないかという話にゃ。
面倒臭いので、l/g = 1とするけれど、
すると、解く方程式は
これは、どんなに頑張っても、解析的に解くことはできない。
簡単そうに見えるけれど、解けない!!
近似的に解く以外に手が無い。
そして、
これは非線形の運動なんだにゃ。
プログラムは、
DEF f(x,y,p) = -y
を
DEF f(x,y,p) = -sin(y)
に変えるだけ。
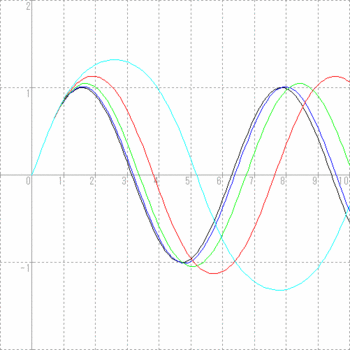
初期条件を
x = 0のとき、y = 0 として、
y' = pの初期値を0.1、0.5、1.0、1.5、1.8と変化させ、
pの初期値(振り子が一番下にあるところの速度で、振り子の振幅に関係がある)が大きくなると、振り子の周期は長くなるんですよ。
振り子の周期は、振幅によって変わるんだにゃ。
振り子の等時性は、振幅が小さいときの近似則なんだケロ。
つまり、
ガリレオは間違っていた!!
y'' - 3y' + 2y = 0 ならば、
p' - 3p + 2y = 0
p' = 3p - 2y
になるので、
f(x,y,p) = 3*p - 2*y
とすればいいし、
y'' - 3xy' + 2y = x + 10 ならば
p' - 3xp + 2y = x + 10
p' = 3xp + x - 2y + 10
になるので、
f(x,y,p) = 3*x*p + x - 2*y + 10
と変えるだけ。
あとは、初期値を与えさえすれば、このプログラムで計算できるけろ。
差分法を用いた二階の常微分方程式の境界値問題のプログラムもそのうちにアップします。
差分法を用いた簡単な偏微分方程式の解法もご紹介するつもりです。
【お知らせ】
ルンゲ=クッタ法を用いて常微分の連立方程式を解く記事を明日6/7に公開する予定です。
ルンゲ=クッタ法で連立微分方程式を解く
上をクリックすると、別窓でこの記事が見られます。
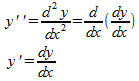
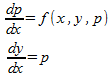
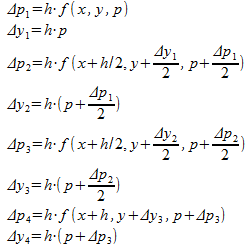
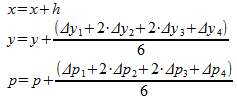




コメント 0