第５回 逆像の性質

第５回　逆像の性質

f:X→Yという写像があり、B⊂Yであるとき
　　

をBのfによる逆像（原像）というんだケロ。

ここまでは、復習だケロ。

で、逆像には関しては次の定理があるんだケロ。

定理　f:A→Bを写像とし、
　　
とするとき、

　　

が成り立つ。

 

前回やった証明は、書く方も読む方も辛いと思うので、次の証明を紹介するにゃ。

【証明】

たぶん、ここに何が書いてあるか、わからないと思うけれど、世の中には人知を超えたものがあるってことだケロ(^^ゞ

逆像に関しては、等号が成り立つということだけを知っていればいいわさ(^^ゞ

なのだけれど、

定理　f:A→Bを写像、
　　
のとき、

　　

である。

と、また、等号が失われてしまうんだケロ。

この証明は後回しにしまして、実例を上げたほうが、これは理解しやすいと思うケロ。

例　f:R→Rで、

　　

という写像を考えるケロ。

で、A=[0,2]とすると、
　　f(A)=f([0,2])=[0,4]

となる。

一方、
　　

となるケロ。

[0,2]⊂[-2,2]だから、
　　

となるんだケロ。

で、B=[-1,4]とすると、
　　

になる。

で、
　　

となるんだにゃ。

で、何故、等号が成立しないかというと、（１）の場合はfが単射じゃないから、そして、（２）の場合は全射じゃないから。

ということで、「写像が単射か、全射か」ということはとっても大切なんだケロ。

証明は、

　　

とやるんだケロ。

（２）もほとんど明らかなんで・・・。

とする。

すると、写像の定義から、b=f(a)となる
　　
が存在する。
よって、
　　
となり、
　　

本によっては、（１）、（２）ともに「明らか」の一言で片付けている(^^)

あまりに明らかなので、証明の内容はかえって理解を拒む(^^ゞ

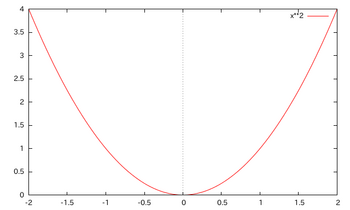
この包含関係に迷った時は、二次関数
　　
を思い浮かべるといいですよ。

前回の第４回、そして、今回の定理は、正直、微分積分では使わないのだけれど、

これは位相という「何だかわからないの数学の分野」を勉強するとき、これを使うんだケロ。

そして、

一年後くらいには、位相をやるんじゃないか。

第４回、第５回で大切なのはイメージです。

写像の像はイメージ（image）だ！！

そして、何か困った時、判断がつかない時には

　　

の３つの関数を思い浮かべれば、大体、事足ります。