第１５回 ３重積分の応用・体積

第１５回　３重積分の応用・体積

高校の数学で、立体Ωの体積Vは、zにおけるΩの断面積をS(ｚ)とすると、

　　

で求められると習ったと思うにゃ。

立体Ωが

　　

で与えられるとすると、

　　

となる。
はｚにおける立体の断面積になるので、この３重積分の計算は立体Ωの体積を計算したことに相当する。

ということで、次の定理がえられる。

定理
関数f(x,y)、g(x,y)が積分領域Dで連続で、f(x,y)≦g(x,y)であるとする。このとき、D上のｚ軸方向の柱体z=f(x,y)、z=g(x,y)が囲むΩの体積Vは次で与えられる。
　　

【証明】

立体Ωは
　　
縦線集合とあらわせるので、体積Vは３重積分を累次化すると

　　

となる。


問題１　放物面と曲面で囲まれた体積を求めよ。

【解】

グラフにするとこんな感じになる。

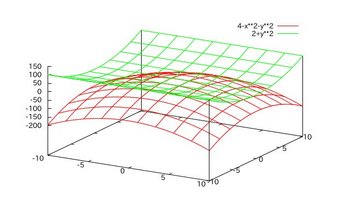
分かりづらいと思うけれど、求める立体Ωは

　　

だにゃ。

x=0、y=0を入れると、曲面の上下関係がわかると思う。

で、Dは

　　

なので、

　　

となるのだけれど、こんな計算はしたくない。

そこで、

　　

となるので、少し工夫し、x=√2rcosθ、y=rsinθと置くと、Dは

　　

になる。

この時のヤコビアンJは
　　
から、J=√2rとなり、よって
　　

計算のテクニックですね。

問題２　２平面、z=0とz=2–yと円柱面で囲まれる部分の体積を求めよ。

【解】

立体Ωは

　　

となる。

で、

　　

となり、これをお決まりの極座標で変換すると、積分領域は

　　

となるので、

　　

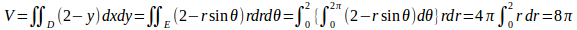
タグ：重積分