第？回 問題演習

第？回　問題演習

第０回の内容に関する問題演習をすることにするにゃ。

問題１　次の集合はどの演算について閉じているか。

（１）　N=｛自然数｝　　（２）　P=｛３で割って１余る整数｝

（３）　X=｛係数が整数である２次以下の整式｝

【解】

（１）　n、mを自然数とすると、n+mは自然数になるので、つまり、n+m∈Nだから、加法・足し算については閉じている。

引き算・減法については、n=1、m=2とすると、1−2=−1となり、これは自然数ではないので、閉じていない。

乗法・掛け算については、n×m∈Nだから、閉じている。

除法・割り算については、n=1、m=2とすると、n÷m=1/2=0.5になるので、閉じていない。

よって、閉じているのは、加法と乗法。

（２）　３で割って１余る整数は、ある整数kがあって、3k+1とあらわすことができる。

ということで、

　　加法　(3n+1)+(3m+1)= 3(n+m)+2　・・・　余りは２

　　乗法　(3n+1)×(3m+1)= 9nm+3(n+m)+1　・・・　余りは１

　　減法　(3n+1)−(3m+1)=3(n−m)　・・・　余りは０

　　除法　4÷1=4　・・・　余りは０

となり、乗法以外成り立たないことが分かる。

（３）　加法、減法については閉じている。

　　

a₀、a₁、a₂とb₀、b₁、b₂がが整数ならば、上の式の係数はすべて整数になるからだにゃ。

乗法、除法については、x×x²=x³、
x÷x²=1/xなどが反例として挙げられ、乗法、除法については閉じていない。

問題２　実数全体の集合において、演算*を次のように定める。この演算は交換法則が成り立つか。また、結合法則は成り立つか。

　　

【解】

交換法則

　　

結合法則

　　

よって、結合法則は、一般に成立しない。

問題３　次の【Ⅰ】、【Ⅱ】が成り立つことを証明せよ。

　　

これを用い次の２重根号をはずせ。

　　

【解】

証明には、因数分解の次の公式を使うにゃ。

　　

p=√a、q=√qとおくと、上の式は

　　

よって、

　　

ということで、

a>0、b>0のとき

　　

a>b>0のとき、

　　

（１）　a+b=7、ab=10になるaとbを見つけるにゃ。そうすると、(a,b)=(2,5)または(a,b)=(5,2)になる。

どっち使ってもいいけれど、(a,b)=(2,5)を使うと、

　　

となるにゃ。

（２）　a+b=15、ab= 50、そして、a>b>0になるaとbを見つけるにゃ。そうすると、a=10、b=5。

だから、

　　

となる。

（３）　これは

　　

となるので、・・・。

あとは、自分でやるべきだにゃ。

問題４　有理数a、bを用いて、a+b√2と書ける数全体の集合をAとする。次の数がAに属するかどうか判定せよ。

　　

【解】

（１）　これは、a=−2/3、b=0だから、Aに属する。

（２）　これは、

　　

となり、Aに属するにゃ。

（３）　これは、難問かもしれない(^^)

√3がAに属するならば、√3=a+b√2となる有理数a、bが存在する。

　　

⑨の左辺は有理数だから、⑨が成立するためにはa=0でなければならない。

　――a≠0だと、左辺は有理数、右辺は無理数になる！！――

よって、

　　

となり、bは無理数になる。

bが有理数という仮定と矛盾するので、√3=a+b√2とあらわせる有理数は存在しない。

よって、√3はAに属さない。

背理法ってやつだにゃ。

√3や√6が無理数であることを使って駄目ということになると、この証明までしなければならなくなる。どこまで既知として使っていいのかわからないにゃ。

（４）　これは

　　

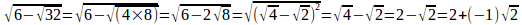
となるので、Aに属する。

「⑨が成立するために、a=0でなければならない」としたけれど、これは証明すべきことなのかもしれない。

ということで、

問題　p、qが有理数で、p+q√3=0であるならば、p=q=0であることを証明せよ。ただし、√3が無理数であることを用いてよい。

【解】

q≠0と仮定すると、

　　
左辺は無理数、右辺の有理数になってしまうので、q=0。

q=0をp+q√3=0に代入すると、p=0。

よって、p=q=0である。

タグ：中学数学