第６回 中点連結定理

第６回　中点連結定理

定理９　中点連結定理

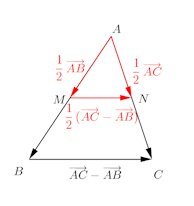
△ABCにおいて

辺AB、ACの中点をそれぞれM、Nとすれば

逆も成り立つ。



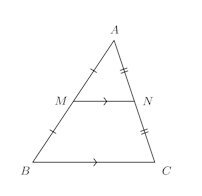
【証明】

証明は、次の図のようにMNを２倍に延長し、その端点をLとし、MとC、AとLを直線で結ぶ。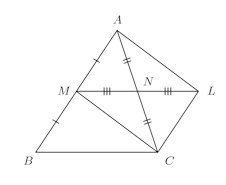

仮定より、

　　MN=NM

　　AN=NC

よって、四角形AMCLの対角線を互いに２等分しており、四角形AMCLは平行四辺形。

四角形AMCLは平行四辺形だから、

　　LCとAMは平行でかつAM=LC。

LCはAMに平行だから、MNにも平行。

また、仮定より

　　MB=AM=LC

よって、四角形MBCLは平行四辺形。

したがって、

　　

かつ

　　

（逆の証明）

　　

また、

　　

よって、四角形MBCLは平行四辺形。

　　

BAとCLは平行なので

　　∠AMN=∠LCM

　　∠NAM=∠NLC

また、

　　MN=LN

よって

　　△NAM≡△NCL

したがって

　　AM=CL=MB

　　AN=NC

ということで、

　　

ならば、MはACの中点、NはABの中点となり、証明された。

（証明終わり）

ベクトルによる証明は、循環論法の疑いがあり、証明になるかどうか怪しいけれど、

　　

よって、

　　

定理１０　中線連結定理２

△ABCにおいて

辺ABの中点MからBCに平行線をひけば、辺ACの中点を通る。

【証明】
辺ABの中点Mを通るBCに平行な直線とACの交点をNとする。

NをとおるABに平行な直線を引き、BCとの交点をLとする。

四角形MBLNは平行四辺形で、対辺の長さは等しいから、

　　NL=MB=AM

ABとNL、ACとMNは平行なので

　　∠NLC=∠B=∠AMN　（同位角）

BCとMNは平行なので

　　∠LCN=∠MNA　（同位角）

よって、

　　△AMN≡△NLC　（１辺と両端の角相等）

よって、

　　AN=NC

NはACの中点である。

（証明終わり）

例題

４角形の対角線の中点を結ぶ線分と対辺の中点を結ぶ線分とは互いに他を２等分することを証明せよ。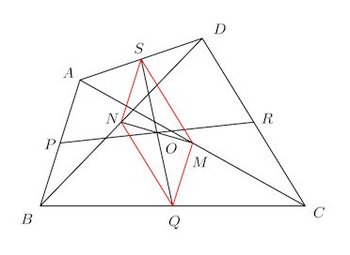

【証明】

４角形をABCDとし、図のように辺AB、BC、CDの中点をP、Q、R、Sとする。また、対角線AC、BDの中点をそれぞれM、Nとする。
SがADの中点、NがBDの中点であるから、

　　

また、MがACの中点、QがBCの中点だから

　　

よって

　　

よって、４角形SNQMは平行４辺形。

ゆえに対角線SQとMNとは互いに他を２等分する。

同様に、４角形PMRNは平行四辺形だから、PRとMNも互いを２等分する。

問題　平行四辺形ABCDの辺AD、BCの中点をそれぞれE、Fとすれば、BE、DFはACを３等分することを証明せよ。

【証明】

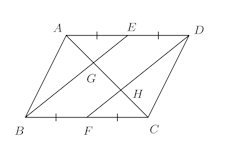
平行四辺形なので、

　　

故に、

　　

よって、四角形BFDEは平行四辺形。

したがって、

　　

△AHDに注目。

EはADの中点なので、中点連結定理２よりGはAHの中点。

よって、

　　AG=GH

△BCGに注目。

同様に、HはGCの中点で、

　　GH=HC

よって、

　　AG=GH=HC

したがって、BE、DFはACを３等分する。
（証明終わり）

タグ：初等幾何