第２１回 三角形の辺と角の大小２

第２１回　三角形の辺と角の大小２

§１　正弦定理、再び

三角関数でやった正弦定理を覚えているケロか。

正弦定理

　　

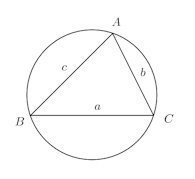
この正弦定理を使うと、

　　

を証明することができる。

まず、△ABCが鋭角三角形、または、直角三角形（∠C=90°）の場合を考える。

正弦定理から

　　

になる。

ここで、正弦関数y=sinx（0<x<π）のグラフを思い出して欲しい。グラフをかくと次のようになる。

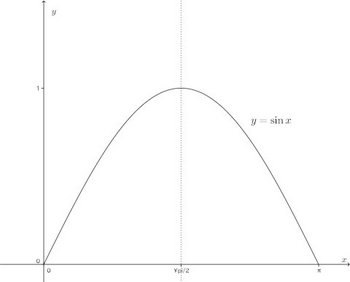
このグラフから明らかなように、0<x≦π/2では正弦関数は単調増加で、π/2<x<πで単調減少になっている。

つまり、0<x≦π/2では、

　　

が成立する。

だから、

　　

となる。

問題は、鈍角三角形。議論を簡単にするために、△ABCの最大角を∠C>90°=π/2とする。

三角関数の角関係より

　　

が成立する。

こうすると、

　　

となる。

もしこのとき0<B<π/2<C<πで

　　

ということが起きたとする。

すると、このとき、

　　

となり、△ABCの内角の和が180°を超してしまう。

だから、鈍角三角形の場合も

　　

が成立し、これと正弦定理を合わせると

　　

が成立する。

よって、△ABCでは

　　

である。

三角関数の正弦定理を使っても証明できるという話でした。

§２　三平方の定理、再び

問題　△ABCにおいて

であることを証明せよ。

また、（１）、（２）の逆も成立することを証明せよ。

この問題は、余弦定理のところでも解いているのですが、初等幾何では三角比や三角関数を使わないという鉄則があるので、あらためて初等幾何の範囲内でこのことを証明することにする。

【証明】

∠A=R、A'B'=AB、A'C'=ABとなる直角三角形があるとする。

△A'B'C'は直角三角形なので

　　

（１）　△ABCのAとBを△A'B'C'のA'B'に重ねる。

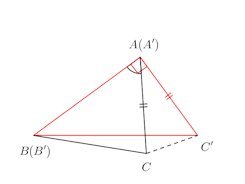
△ABCと△A'B'C'において∠A<∠A'=∠Rだから、第１９回の定理BよりBC<B'C'。

よって、

　　

（２）　同様に、△ABCと△A'B'C'において∠A>∠A'=∠RだからBC>B'C'。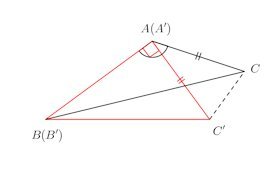

よって、

　　

（証明終わり）

 

【逆の証明】

三平方の定理と上の（１）と（２）から

　　

①、②、③の仮定はすべての場合を尽くしており、その結論は、それぞれ、そのほかの結論と両立し得ない。

よって、転換法より、①、②、③の逆が成立する。

【証明終わり】

タグ：初等幾何 三角関数