定積分で表された関数２

定積分で表された関数２

問題１　xの関数

　　

の極値を調べ、y=F(x)のグラフの概形をかけ。

【解】

xで微分すると

　　

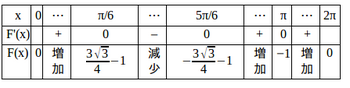
0≦x≦2πでになるのは、sinx=−1になるのはx=π。

　　

F(x)の増減表は
　　
よって、

　　

よって、グラフは次の通り。

（解答終了）

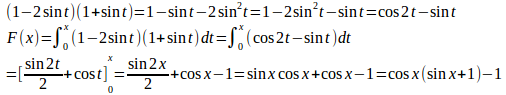
問題２　次の関数の最大値、最小値を求めよ。

【解】

　　

とすると、
　　
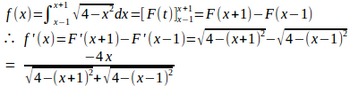
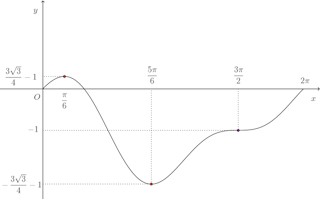
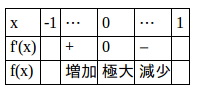
よって、増減表は

　　

t=2sinθ（−π/2≦θ≦π/2）とおくと、

　　

よって、
　　

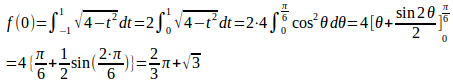
は偶関数だから

　　

また、
　　

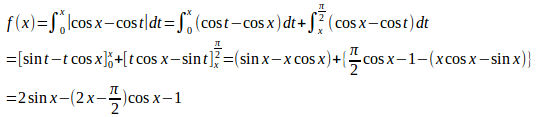
よって、

x=0のとき最大で、最大値は

x=±1のとき最小で、最小値はπ

（解答終わり）

問題３　0≦x≦π/2において

　　

と定義される関数f(x)の最小値をを求めよ。

【解】

　　

だから、
　　　　

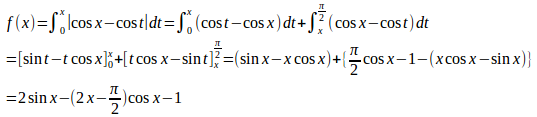
よって、

　　

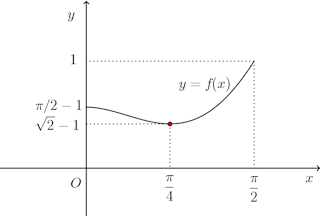増減表を書くと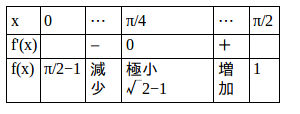

よって、x=π/4のとき最小で、最小値はf(π/4)=√2−1

（解答終わり）

この問題３の類題は大学入試に何度も出ている。

例えば、

 

類題１　a>0のとき、

　　

を最小にするaを求めよ。

（答）

　　

問題４　a≦x≦bにおいてf'(x)<0である関数f(x)に対して、

　　

は、のときに最小になることを証明せよ。

【略証】
　　

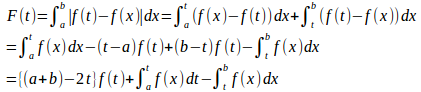
a≦x≦bにおいてf'(x)<0だから、f(x)はa≦x≦bで単調減少。

tで微分すると

　　

よって、のときに極小、かつ、最小。

（略証終わり）

f'(x)>0の場合の証明も行っている。

そして、問題３、類題は、この問題４の特殊な場合。

 

問題５　f(t)がt≧0において連続な関数であるとき、

　　

はx>0において増加関数であることを証明せよ。

【解】

　　

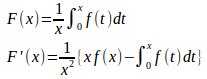
f(t)はt≧0で増加関数だから、0<t<xではf(t)<f(x)

したがって、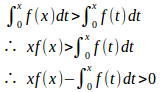
　　

よって、x>0では

　　

で、F(x)は増加関数である。

（解答終了）

この問題は、さらに次のように一般化することができる。

関数f(x)が[a,b]で連続な増加関数ならば

　　

はa<x<bで増加関数である。