ネムネコ、熱伝導方程式を解く

ネムネコ、熱伝導方程式を解く

解く偏微分方程式は

　　

T(x,y)=X(x)Y(t)とおき、（１）に代入すると

　　

（２）式の左辺はtだけの関数、右辺はxだけの関数。

したがって、これは定数。

そこで、次のようにおく。

　　

pは定数。

なんで−p²にするかというと、そうしないと、境界条件からX(x)=0になってしまうから。

これを解くと

　　

T(0,t)=0だから、

　　

また、T(L,t)=0だから、

　　

何故ならば、A=0だと、X=0となり、解として不適だから。

よって、

　　

となるといいのだけれど、そうは問屋が許さない。

この解は、

　　

という形になる。

何故ならば、

　　

は、すべて、（１）を満たすから。

では、どうやって、係数を定めるかというと、フーリエ級数というものを使う。

フーリエ級数については、来年の夏くらいにやるとして、結果だけを述べると、t=0の境界条件、T(x,0)=x(L−x)から定まる。

　　

nが偶数のときcosnπ=1となり、nが奇数のときはcosnπ=−1になるから、nが偶数のときとなる。

ということで、

　　

少し事情があって、L=4の場合で計算すると、

　　

ということで、くらいで計算しても誤差はあまり大きくない。

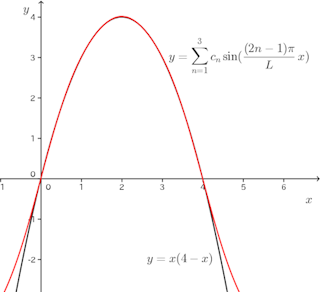
右の図を見ると、を使って計算をすると、[0,4]でy=x(4−x)をほとんど正確に再現していることがわかる。

なんで、L=4のときを計算したかというと、昨夜、ネムネコが書いた数学の記事に関係するんだにゃ。

ネムネコが昨夜、表計算ソフトで解いた熱伝導方程式の厳密解、解析解は、上の式にκ=1/2、L=4を代入すると、

　　

アソコでの計算は、Δt=1、Δx=1という数値計算をする場合あり得ないものだったけれど、この解析解と比較すると、結構、いい値が出ている。誤差、マックス１００％くらい(^^ゞ

t=1、x=1の厳密解が約T≒2.14だから意外に正しいんだケロよ、あの計算。

tが増加するに連れて、誤差が蓄積して１００％くらい値が違うようになるけれど、意外に正しい、あの計算は。

もっとひどい結果が出ることを期待していたのだが、予想に反していたのに・・・。