陽解法による拡散方程式の解法の安定性

陽解法による拡散方程式の解法の安定性

次の拡散方程式がある。

　　

ここで、uは時刻tと位置xの関数、すなわち

　　

とする。
陽解法は（１）を次の差分方程式に置き換えて、次の差分方程式を解くことによって（１）の近似解を求める。

　　

とおくと、（２）は

　　

差分方程式（２）の厳密解は（３）を満たすので、誤差も（３）を満たすと考えられる。
つまり、

　　

誤差が次のように表せるとすると、

　　

（４）より

　　

オイラーの公式より

　　

だから、

　　

さらに、半角公式

　　

より

　　

で、

　　

だから、 （５）式の右辺は誤差の倍率をあらわすと考えられる。

したがって、

　　

のときに、は収束する。

で、

　　

とおくと、

　　

を満たすKは

　　

したがって、

　　

これをすべてのkについて満たさなければならないから、

　　

上の議論は正確なものではないので注意。

このようにして、陽解法の

　　

という制限、条件が出てくるという話です。

さてさて、この話は本当かということで、この検証のためのスプレッドシートを作り、実験してみた。

解く偏微分方程式は、

　　

これをΔt=0.25、Δx=0.5で解いた結果はこれ。
x=1とx=2の計算結果を示してある。

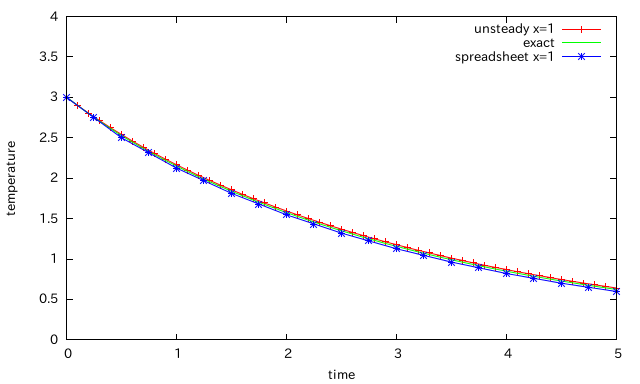
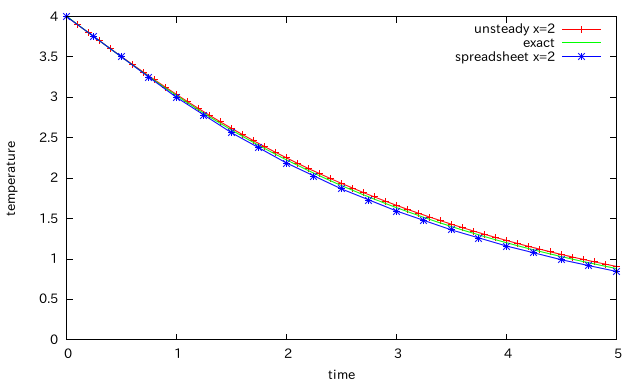
厳密解、そして、陰解法で解いた結果と良好な一致を見せており、このスプレッドシートの正当性を示している。

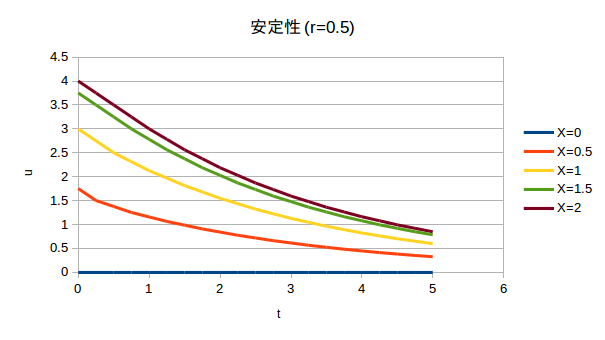
r=0.5の場合

r=0.6の場合。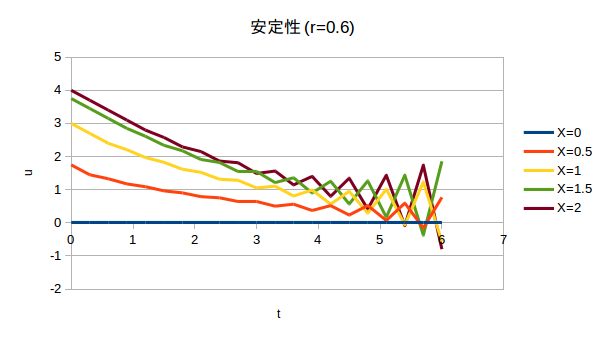



時間の経過とともに誤差が次々と伝播、増大し、数値解が激しく振動してしまう。

タグ：微分積分