体積 座標軸以外の直線のまわりの回転 [ネコ騙し数学]
体積 座標軸以外の直線のまわりの回転
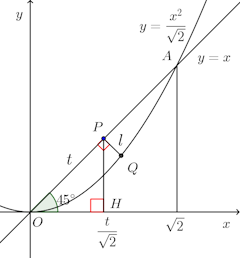
(1) 直線y=x上で原点からの距離がtである点をPとし、Pをとおりy=xに直交する平面でこの立体を切った切り口の面積S(t)を求めよ。
(2) この立体の体積を求めよ。【解】
(1) Pからx軸におろした垂線の足をH、Pを通りy=xに直交する直線と曲線y=x²/√2との交点をQとする。OP=tだから、Pの座標は
よって、点Qの座標は
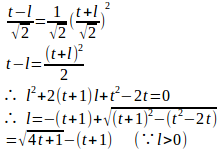
よって、切り口の面積S(t)は
(2) y=xとは原点Oと点A(√2,√2)で交わり、したがって、OA=2。
ここで、
で、とおくと、t=0にはu=1、t=2にはu=3が対応する。
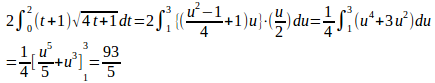
ゆえに、
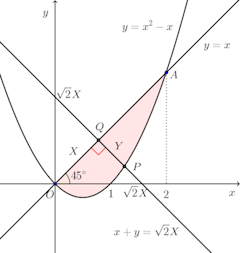
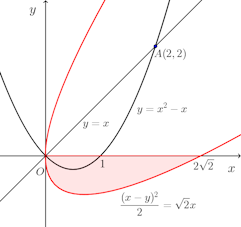 問題2 放物線y=x²−xと直線y=xとで囲まれた部分が、この直線のまわりに回転してできる立体の体積を求めよ。
問題2 放物線y=x²−xと直線y=xとで囲まれた部分が、この直線のまわりに回転してできる立体の体積を求めよ。
【解】
①をyについて解くと、
回転を利用すれば上の解答のように解くことができるが、次のように解くこともできる。
放物線y=x²−xと直線y=xの交点は原点OとA(2,2)。
曲線上の点P(x,y)からy=xにおろした交点をQ、
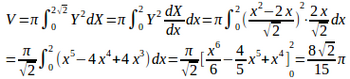
(解答終了)
あまりいい解き方ではないが、次のような解答を作ることもできるだろう。
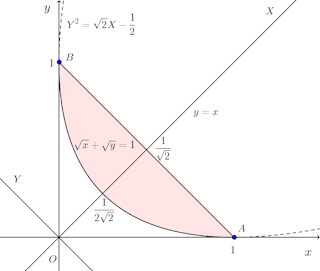
問題3 と座標軸とが囲む部分が点A(1,0)、B(0,1)を通る直線のまわりに一回転してできる立体の体積を求めよ。
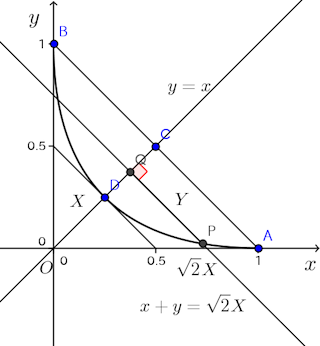 【解】
【解】は、媒介変数tを用いて
P(t³,1−2t+t²)からy=xにおろした垂線の足をQとし、
(解答終了)
これよりは、次のように解いたほうがいいだろう。
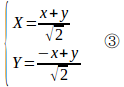
と変数を変換すると、②は
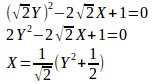
になる。
つまり、曲線①の正体は放物線の一部ということが分かる。
そして、このことを利用すると、次の問題を解くことができる。
【解】
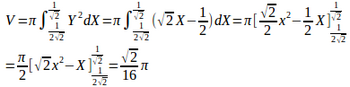
(解答終了)
2016-11-26 12:00
nice!(0)
コメント(0)
トラックバック(0)




コメント 0