ワンポイントゼミ２６

ワンポイントゼミ２６

ねこ騙し数学の記事の中では

　　

と書いたけれど、この不等式は

　　

の方がいいのかもしれないね。

ちなみに、n！とは

　　

のこと。

ということで、

　　

である。

また、定義から

　　

という関係がある。

　　

になっているからね。

そして、さらに0！を

　　

と定義する。

そうすると、

　　

で、0のときにも①が成立することになる。

n=1のとき1!=2⁰

n=2のとき2!=2¹

だから、①の不等式で等号が成立する。

n≧3では、⑨が成立する。

この証明は、ねこ騙し数学の記事に書いてある。

ということで、

となる。

 

また

　　

である。

　　

になっている。

n=4のとき

　　

だから（１）は成立。

n=kのとき

　　

が成立するとする。

n=k+1のとき

　　

よって、数学的帰納法より（１）が成立する。

では、ここで一つ問題！！

問題

n、mを１より大きい整数とする。

このとき、

　　

を満たすｎとｍを求めよ。

【答】

(n,m)=(2,4)、または、(n,m)=(4,2)

2⁴=4²=16だからね〜。

しかし、これでは数学の解答にならない！！

今日のねこ騙し数学の記事がヒントだにゃ。

②の両辺の対数をとる。

そうすると、

　　

n≠0、m≠0だから、nmで両辺を割ると

　　

ということで、

　　

という関数が出てくる。

で、とりあえず、n≦mとする。

そうすれば、

　　

となり、

　　

というxの解の個数を求める問題に帰着できる。

f(x)を微分して、この増減を調べる。

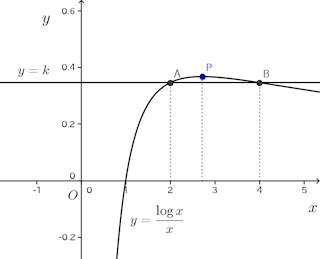
そすると、この関数はx<eで増加、x>eで増加するから、上の方程式が解を２つもつためには、片方の解がx<e<3より小さくなる必要がある。

したがって、1<n<3を満たすnは２しかない！！

だから、n≦mのとき、2⁴=4²の組み合わせしかない。

なのだが、

2⁴=4²または4²=2⁴を知らないヒト、あるいは、これに気づかないヒトはどうするんだろう。
この問題は、大昔、とある私立大学の入試問題として実際に出題されたものだけれど、オレは試験会場でこの組み合わせに気づかないかもしれない(^^ゞ

この問題の解答には

　　「2⁴=4²は4²=2⁴」は既知として・・・

と書いてあったように記憶している。

これは、難関（私立）大学を目指す受験生にとって既知の内容で、「2⁴=4²は4²=2⁴」は絶対に知っておかないといけないことだったのか。

タグ：微分積分