第４回 確率分布２

第４回　確率分布２

分布関数と確率密度関数

変数Xが連続な値をとるとき、Xを連続型の確率変数といい、X<xである確率P(X<x)が

　　

で与えられるとき、F(x)を分布関数といい、その導関数

　　

をxの確率密度関数という。

　　

だから

　　

で、xがある範囲にに存在する確率は、y=f(x)のグラフのその範囲の面積と等しい。

変数Xの変域をa≦x≦bとし、確率密度関数をf(x)、平均をm、分散をσ²とすると、

　　

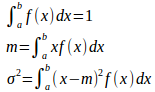
である。

　　

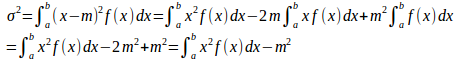
となり、

　　

と書くと、分散V(x)は

　　

になる。

 

問題１　確率変数Xの従う確率分布の密度関数f(x)が

　　

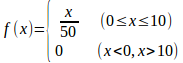
であるとき、次の問いに答えよ。

（１）　P(3≦X≦5)の値を求めよ。

（２）　P(7≦X)の値を求めよ。

（３）　Xの平均E(X)を求めよ。

（４）　Xの標準偏差D(X)を求めよ。

【解】

（解答終了）

問題２　あるバスの停留所の発車時刻は毎時０分、１５分、３５分の３回である。この発車時刻をまったく知らない人が、停留場へ来て待たされる時間の期待値を求めよ。

【解】

この人が停留所に来る時刻をx分とすると、待ち時間tは

　　

確率密度f(x)は一様分布と考えられるので、

　　

とすると、

　　

したがって待ち時間の平均・期待値E(ｔ)は
　　

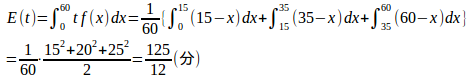
（解答終了）

問題３　連続的な値をとる確率変数xがあって、その確率密度がAを定数として、

　　

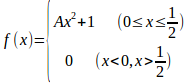
とするとき、となるようなaの値を求めよ。

【解】
　　

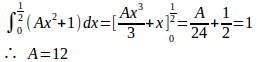
したがって、

　　

a=0.2とすると、

　　

よって、a=0.2

（解答終了）

なのですが、a=0.2であることに気づく人はどれだけいるのだろう。

　　

試験会場で、これはチョット気づかないだろう。

条件より0<a<0.5で、

　　

だから、a=0.2と気づけということか。

とおくと、

　　

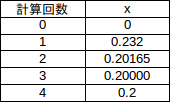だから、ニュートン法

　　

を用い、x₀=0として計算すると、次のようになる。

計算の初期値としてx₀=0.232を選べば、１、２回計算すれば、a=0.2であることに気づくのではないか。

問題４　半径aの円Oの周上の１点Aから任意の方向に弦を引くとき、それらの弦の長さの平均を求めよ。

また、弦の長さが半径より大となる確率を求めよ。

【解】

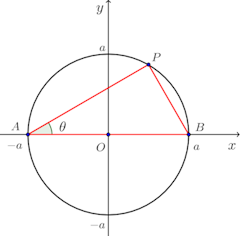円の中心Oを原点、Aを(−a,0)、Bを(a,0)とし、周上の点をPとする。

弦APとx軸のなす角をθ（−π/2≦θ≦θ/2）とすると、弦APの長さlは

　　

θを確率変数とし、一様分布

　　

と仮定すると、

　　

したがって、弦の長さの平均は
　　

AP>aになるのは、

　　

したがって、弦の長さが半径より大きい確率は

　　

（解答終了）