第６０回 複素数関数の２次元流れへの応用

第６０回　複素数関数の２次元流れへの応用

平面上の点(x,y)における流体の速度ベクトル

　　

とし、流体の密度をρ、時刻をtとすると
　　

が成立する。

密度ρが一定のとき、連続の式は

　　

となる。

さらに、流れが渦なしの条件

　　

を満たすとき、前回示したように

　　

である速度ポテンシャルφが存在する。

ここで、

　　

とおき、

　　

となる流れ関数Ψを導入すると、これはコーシー・リーマンの関係になるので、複素関数f(z)は正則で、微分可能であるなる。

つまり、

　　

そして、このように定義された複素関数f(z)を複素速度ポテンシャルという。

Ψ=一定の曲線の勾配（Ψ=一定の曲線の法線ベクトル）は

　　

だから、速度ベクトルVとの内積を取ると
　　

となり、Ψ=一定の曲線は速度ベクトルと平行である。

つまり、Ψ＝一定の曲線は流線である。

例１　一様な流れ

複素速度ポテンシャルが

　　

の場合、

　　

だから、φ=Ux、Ψ=Uyとなる。

また、

　　

だから、u=U、v=0となり、x軸に平行な速度一定の流れということになる。

 

例２

複素速度ポテンシャルが

　　

の場合は、

　　

したがって、φ=x²−y²、Ψ=2xy。

そして、複素速度は

　　

だから、速度のx成分u=2x、y成分v=−2yとなる。

したがって、流線の方程式は

　　

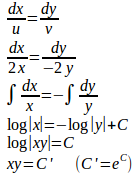
ということになる。

　――流れ関数Ψ=2xy=一定の曲線と上で求めた流線の方程式は一致していることがわかる！！――

流線の接線は流れの速度の方向と同じなので、この流れはx軸とy軸を壁とする流れを表している。

 

例３

　　

とおくと

　　

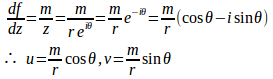
また、
　　

また、

　　

だから、この流れは原点と点zを結ぶ（半）直線と平行で、流線は原点を通る放射線群である。

速度ベクトルの大きさは

　　

だから、速さは原点からの距離に反比例する。

また、原点を中心とする半径Rの円Cに流れ込み、そして、流出してゆく量、湧出量Qは、

　　

で、半径に関係なく一定である。

m>0のときは吹き出し、m<0のときは吸い込みである。

例４

　　

とおくと

　　

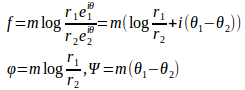
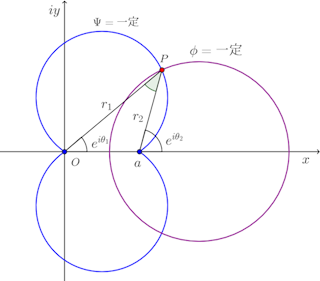
流線（流れ関数Ψ=一定）上の点をPとすれば、∠OPa=θ₁−θ₂=一定だから、流線は原点Oと点aを通る円弧となる。

また、等ポテンシャル線はr₁/r₂が一定だからアポロニウスの円である。

また、

　　

だから、点aに強さmの吹き出し、原点に強さmの吸い込みがある場合と考えることもできる。

タグ：複素解析 ベクトル解析