第20回 数列の極限とその定理 [ネコ騙し数学]
第20回 数列の極限とその定理
数列
自然数全体の集合をNで表す。すなわち、N={1, 2, 3, ・・・, n, ・・・}。
自然数Nから実数Rへの写像を実数列、または、数列といい、記号
![]() あるいは単に
あるいは単に![]() で表す。これは実数を
で表す。これは実数をと並べたものである。
数列の収束
数列![]() が次の条件を満たすときα∈Rが存在するとき、
が次の条件を満たすときα∈Rが存在するとき、![]() はαに収束するという。
はαに収束するという。
任意のε>0に対して、あるmが存在して、
である。
定理1 (数列の極限の一意性)
【証明】
また、
とすると、ある正の整数m₂があって
よって、m=max{m₁,m₂}とすると、任意のε>0に対して
となり、|α–β|=0となり、α=β。
(証明終)
定理2 (収束数列の有界性)
【証明】
ある1つの値にε>0をとると、ある正の整数mがあって、n>mならば
である。
そこで、
の最大値をMとすると、
よって、収束する数列は有界である。
(証明終)
定理3 (数列の極限の大小)
数列は収束し、
であるならば、
である。
【証明】
任意のとおくと、
より、ある正の整数m₁があって
より、ある正の整数m₂があって
よって、m=max{m₁,m₂}にとると、n>mならば
となり、に矛盾。
ゆえに、α≦βである。
(証明終)
定理4 (数列の極限の公式)
定理5 (ハサミ打ちの定理)
すべての正の整数nについてで、かつ、
ならば、
である。
【証明】
![]() より、任意のε>0に対して、ある正の整数m₁があって、n>m₁ならば
より、任意のε>0に対して、ある正の整数m₁があって、n>m₁ならば
より、任意のε>0に対して、ある正の整数m₂があって、n>m₂ならば
また、だから、m=mas{m₁,m₂}にとると、
よって、である。
(証明終了)
定理6 (有界な単調数列の収束性)
![]() が単調増加数列かつ上に有界(単調減少数列かつ下に有界)ならば
が単調増加数列かつ上に有界(単調減少数列かつ下に有界)ならば![]() は収束する。
は収束する。
【証明】
上に有界な単調増加数列の場合について証明する。
したがって、
で、かつ、任意のε>0に対して
であるmが存在する。
したがって、n>mならば
よって、
下に有界な単調減少数列の場合も同様。
(証明終)
定理7
【証明】
条件より、![]() は上に有界な単調増加数列、
は上に有界な単調増加数列、は下に有界な単調減少数列。よって、定理6より、
![]() は収束する。
は収束する。
とおくと、定理3よりα≦β。
よって
したがって、
【証明終了】
定理8 (区間縮小法)
閉区間の列において
ならば、すべての閉区間に含まれる1点αが存在し、
である。
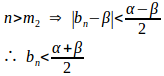
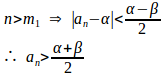
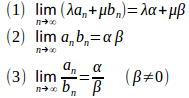




コメント 0