レムニスケート [ネコ騙し数学]
レムニスケート
問題1 2定点(−a,0)、(a,0)からの距離の積がa²である点Pの軌跡を求めよ。ただし、(a>0)とする。
【解】
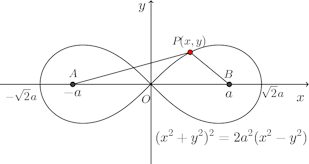 2定点をA(−a,0)、B(a,0)とし、点Pの座標を(x,y)とすると、
2定点をA(−a,0)、B(a,0)とし、点Pの座標を(x,y)とすると、
また、
よって、
(解答終)
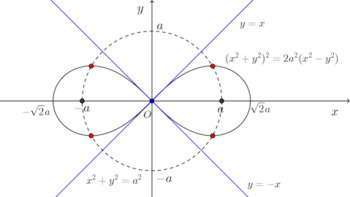
問題で求めた点Pの軌跡(曲線)
をレムニスケート(lemniscate)という。
x=rcosθ、y=rsinθとおき、(1)を極座標を用いて書き直すと、レムニスケートは
になる。
さらに、(2)を用いると、レムニスケートによって囲まれる領域の面積Sを
と求めることができる。
問題2
関係式(x²+y²)²=2a²(x²–y²)(a>0)で定まるxの陰関数yの極値を求めよ。
【解】
(x²+y²)²=2a²(x²–y²)の両辺をxで微分すると、
x=0では極値を取らないから、x²+y²=a²でなければならない。
そこで、(x²+y²)²=2a²(x²–y²)にy²=a²–x²を代入すると、
(解答終(?))
上の計算からわかるように、極値を取る点はレムニスケート(x²+y²)²=2a²(x²–y²)と原点を中心とする半径aの円x²+y²=a²の交点である。
原点(0,0)における接線はy=x、y=−xの2本で、原点は結節点である。
うるさいことを言えばで極値になることを示すために、
における2次微分係数y''の値を調べる必要があるけれど、計算が複雑になるので、この吟味は省略した。
ただ、微分積分を使わずに、極座標を用いて次のように解くこともできるだろう。
【別解】
三角関数の倍角公式より
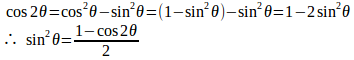
これを(3)式に代入すると
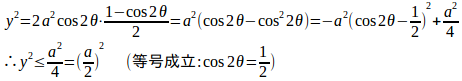
0≦2θ<π/2=90°とすると、θ=π/6=30°のときに、yは最大値a/2をとる。
このとき、
だから、
この曲線はx軸、y軸、原点に関して対称だから、極値は
(別解終(?))
問題3
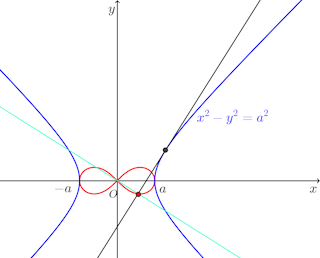
(1) 曲線x²–y²=a²(a>0)の(x₀,y₀)における接線を求めよ。
(2) (1)で求めた接線に原点Oから下ろした垂線の足の軌跡を求めよ。
【解】
(1) x²–y²=a²の両辺をxで微分すると、
よって、曲線上の点を(x₀,y₀)とするとき、y₀≠0のとき、接線の方程式は
接線の方程式は、y=0、x=−aのときx=−a、y=0、x=aのときx=aとなるが、この場合も⑨式で表せるので、
 (2) 曲線上の点(x₀,y₀)における曲線の接線の方程式は、x₀x–y₀y=a²だから、原点Oを通りこの接線に垂直な直線の方程式は、
(2) 曲線上の点(x₀,y₀)における曲線の接線の方程式は、x₀x–y₀y=a²だから、原点Oを通りこの接線に垂直な直線の方程式は、
したがって、垂線の足の座標は連立方程式
の解で
よって、
曲線x²–y²=a²上の点(x₀,y₀)をx₀=ρcosθ、y₀=ρsinθとすると、
これを⑨³に代入すると、
となり、軌跡はを焦点とするレムニスケートである。
(解答終)
この他にも、レムニスケートは楕円関数などとも深い関係があるけれど、これは「ねこ騙し数学」の現在のレベルを越えてしまうので、この点については触れないことにする。
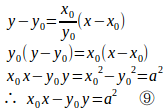
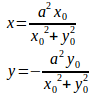
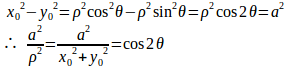




コメント 0