スカラー関数の勾配 [ネコ騙し数学]
スカラー関数の勾配
関数φ(x,y)がC¹級であればf(x,y)は全微分可能で
![]()
あるいは、Δx、Δyをdx、dyに置き換え
で表される。
このとき、ベクトルを関数φの勾配(gradient)といい、記号
などであらわす。すなわち、
![]()
である。
したがって、
とすると、全微分dφは、ベクトルの内積を用いて
とあらわすことができる。
φ(x,y)=c(一定)とすれば、φ(x,y)=cは1つの曲線をあらわす。この曲線上の点P(x₀,y₀)における全微分は
![]()
であり、これは点Pにおける曲線φ(x,y)=cの接線の方程式である。
したがって、
とおけば、曲線φ(x,y)=cの点P(x₀,y₀)における接線の方程式は
となり、これは∇φが曲線φ(x,y)=cと直交していることを表している。つまり、∇φは曲線φ(x,y)=cの法線ベクトルである。
この議論は、そのまま、2次元から3次元へ拡張することができ、C¹級の関数φ(x,y,z)に対して、φの勾配を
を定義する。
そして、
をハミルトン演算子といい、記号(微分演算子)∇をナブラと読む。
曲面φ(x,y,z)=cの点P(x₀,y₀,z₀)における接平面の方程式は
![]()
であり、∇φは曲面φ(x,y,z)=cと直交する。そして、∇φはこの曲面の法線ベクトルである。
特に、z=f(x,y)のとき、φ=f(x,y)–z だから、
曲面z=f(x,y)の点P(x₀,y₀,z₀)における接平面の方程式は、
である。
問 z=x²+xy+2y²の点(1,1,4)における接平面の方程式を求めよ。
【解】
だから、
よって、
(解答終)
なにか冗漫でスッキリしないな。次のように書くべきか。
曲面φ(x,y,z)=cがある。曲面上の点P(x,y,z)を通る曲面上の曲線x=x(t)、y=y(t)、z=z(t)を考えると、φはtの関数である。そこで、tを微分すれば、
である。とすると、
で、これは曲面φ(x,y,z)=cの接線ベクトルである。
したがって、
よって、∇φは曲面φ(x,y,z)=cと直交し、∇φはこの曲面の法線ベクトルである。
問題1 uがx,y,zの関数で、uの関数をf(u)とすれば、
であることを示せ。
【解】
(解答終)
問題2 原点に対する位置ベクトルをrとし、r=|r|とすれば、
であることを示せ。
【解】
(ⅰ) だから、
同様に、
したがって、
(ⅱ)
同様に、
よって、
(別解)
f(r)=1/rとおけば、問題1より
(解答終)
問題3 スカラー関数u(x,y,z)、v(x,y,z)の関数をF(u,v)とするとき、次の式を示せ。
【解】
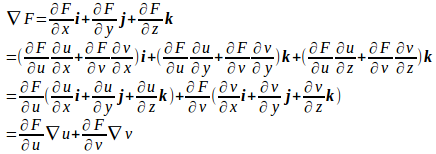
(解答終)
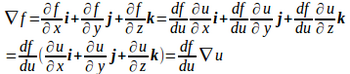




コメント 0