第6回 クレーロー型の微分方程式 [ネコ騙し数学]
第6回 クレーロー型の微分方程式
次の微分方程式
をクレーロー型の微分方程式という。
(1)式の両辺をxで微分すると、
となる。
したがって、p'=0またはx+f'(p)=0である。
p'=0のとき、pは定数だからこれをcとおくと、
となり、これが一般解である。
また、x+f'(p)=0、すなわち、x=−f'(p)のとき、
で、これは特異解である。
以上より、クレーローがの微分方程式(1)の解は、
である。
問1 次の微分方程式を解け。ただし、とする。
【解】
(1) y=px+p²の両辺をxで微分すると、
p'=0のとき、pは定数だからこれをp=cとおくと、一般解は
x+2p=0のとき、x=−2pとなり、これを用いて微分方程式y=px+p²からpを消去すると、特異解は
(2) 微分方程式の両辺をxで微分すると、
よって、p'=0のとき、
のとき、
したがって、
(解答終了)
クレーロー型の微分方程式の特異解は、一般解の包絡線である。
包絡線
αをパラメータとする曲線群f(x,y,α)=0の各曲線とただ1点で接する(共通接線)を曲線を、この曲線群の包絡線という。
f(x,y,α)を3変数のC¹級の関数とすると、曲線群f(x,y,α)=0の包絡線は、2曲線
の交点の軌跡で、この2式からαを消去した曲線に含まれる。
問2 次の曲線群の包絡線を求めよ。
【解】
(1) y=αx+α²の両辺をαで偏微分すると、
αを消去すると、
よって、包絡線は
(2) の両辺をαで偏微分すると、
よって、
![]()
したがって、包絡線は
(解答終)
以上のことより、問1のクレーロー型の微分方程式の特異解が一般解の包絡線になっていることが分かるだろう。
問3 クレーロー型の微分方程式
の特異解の表す曲線は、一般解y=cx+f(c)が表す直線族の包絡線であることを示せ。
【解】
のとき
だから直線と曲線は交点を有する。
この点における曲線の接線の勾配は
![]()
だから、直線y=cx+f(c)はこの曲線の接線である。
(解答終)
裏技として、「クレーロー型の微分方程式の一般解がcの代数方程式の場合、その判別式=0が特異解になる」というものがある。
たとえば、問1の(1)の場合、一般解は、y=cx+c²だから、
(2)の場合、一般解はだから両辺をc倍してcy=c²x+1とし、
と特異解を求めることができる。
問4 次の微分方程式を解け。
【解】
y=px+p²の両辺をxで微分すると、
ゆえに、p'=0またはx+3p²=0。
p'=0のとき、p=cで、一般解は
x=−3p²のとき、
この2式からpを消去すると、特異解は
(解答終)
【別解】
一般解はy=cx+c³だから
cについての3次方程式だから、その判別式=0とすると、特異解は
(別解終了)
(※)
3次方程式x³+px+q=0の判別式Dは
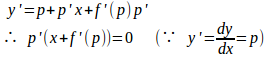
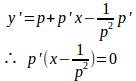
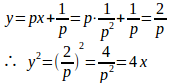
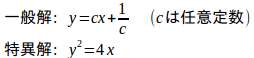
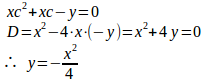
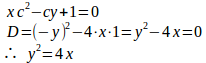
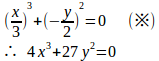




コメント 0