［境界方程式の組み立て（ラプラス型）］

［境界方程式の組み立て（ラプラス型）］

　ここまでで境界方程式（内点方程式）を作成する計算公式は全て出揃ったので、いよいよ境界方程式を組み立てます。

 

　境界方程式と内点方程式は以下でした。

　　

 

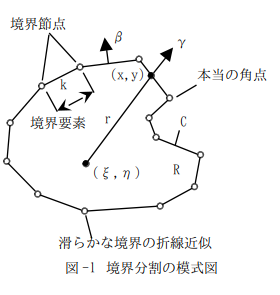
　内点方程式(2)の左辺の境界積分を、図-1の一要素kだけ取り出して書いてやると、境界上でψ(c)とその外法線微分値q(c)を線形近似した場合、

　　

の形になります。

　ψ_jやq_jは、境界要素kの両端点にある境界節点jとj+1でのψ(c)とq(c)の値を表し、これらが未知数です。b_j^(k)やh_j^(k)は、境界要素kの配置と特異点(ξ，η)の位置だけから計算できるのでした。具体的な形は前回にあります。

 

　図-1に示したように、要素kの節点j+1は、隣の要素k+1と共有されるので、そこに注意して(2)の左辺を(3)，(4)を使って書くと、

　　

となります。いま境界要素はn個あり、境界要素と節点は左回りに順序付けられているとします。ψ₁とq₁の係数にb₁⁽ⁿ⁾とh₁⁽ⁿ⁾が現れるのは、要素nと要素1が節点1を共有するからです（図-1）。また境界要素と節点が同数あるのは、図-1から明らかです。式(5)で各ψ_j，q_jの係数を、B_j，H_jと書く事にします。

　　

です（j＝1の場合は、適当に変更して下さい(^^;)）。Σ記号を導入して、

　　

と書けます。一方(2)の右辺はψ^*もgも既知関数なので、なんとかすれば具体的値がわかるだろう、という事で(^^;)、たんにwと書きます。よって、

　　

　ところで内点方程式(2)の目的は、基本解の特異点(ξ，η)を任意に動かして、解析領域R内の任意の位置における未知関数ψの値を、ψ(ξ，η)の形で得る事でした。(ξ，η)の位置が変われば、B_j，H_j，wの値も当然変わります。そこで、(ξ，η)＝(ξ_i，η_i)に取った時の値をB_ij，H_ij，w_iと書く事にします。

　i＝1，2，・・・，[何個でも良い]です。

　そのような意味で式(8)は、

　　

と書くべきだぁ～という事になります。

 

　次に前回の結果から、特異点(ξ_i，η_i)を節点jに近付けて行けば、式(9)左辺のψ_jに関する和、

　　

から自然に、

　　

が導かれ、内点方程式(2)は連続的に境界方程式(1)に移行できるのでした。k_jは、節点jにおける境界の内角です。

　(ξ_i，η_i)→節点jの時のB_ij，H_ijの具体的形も前回の結果で与えられます。一般に式(11)に相当する項は境界要素法では、自由項（free Term）と呼ばれます（←あまり役に立たない蘊蓄(^^;)）。

　(10)，(11)が起きるのは、(ξ_i，η_i)が節点jに一致する時だけだという事に注意し、式(9)を境界方程式として書き直すと、

　　

になりますが、今度は(ξ_i，η_i)がどれかの節点jと一致するので、i＝1，2，・・・，nです。

　なおd_ijは、クロネッカーのデルタです。普通それはδ_ijと書かれますが、今までδはデルタ関数や変分の意味にさんざん使ってきたので、ここはdにしました(^^;)。

 

　式(12)をさらに整理するために突然ですが、行列とベクトルの積を思い出して下さい。行列A＝(a_ij)とベクトルx＝(x_i)との積は、

　　

って書きますよね？。これを成分で書くと、

　　

ですよね？。・・・式(12)と同じじゃないですか！(^^)。

　　

です。

　さらに、

　　

と以後略記します。(14)で行列はn×nの正方行列、ベクトルの次元は必ずnです。

　　

　形式的には式(15)が、境界節点で離散化して組み立てられた境界方程式の全てです。ψとqの係数行列BとHは既知であり、wも既知ベクトルです。後は(15)を、ψとqに関する連立一次方程式とみなして解けば良い訳ですが、なお留意点がいくつかあります。

 

タグ：境界要素法 数値解析