材料力学のお話2 [ネコ騙し数学]
材料力学のお話2
このとき、直交座標系O-x₁x₂に関する応力テンソルTの成分は
となる。
直交座標系O-x₁x₂を原点Oを中心に反時計回りにθ回転させた直交座標をO-x'₁x'₂をとすると、x'₁軸、x'₂軸の方向余弦は
だから、
とおくと、座標系の変換によって応力テンソルの変換式は
となる。
したがって、
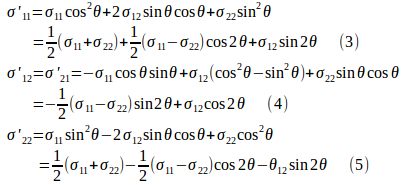
になる。
問1 直交座標系O-x₁x₂に関する応力テンソルが
であるとする。
原点を中心に座標軸を反時計回りにθ回転させたたとき、応力テンソルの成分はどのようになるか。
【解】
(解答終)
問2 直交座標系O-x₁x₂に関する応力テンソルが
であるとする。
原点を中心に座標軸を反時計回りに45°回転させたたとき、応力テンソルの成分はどのようになるか。
【解】
(解答終)
問2のように、単純せん断応力の場合、軸を45°回転すると、応力テンソルからせん断応力を消すことができる。
のとき、応力テンソルの成分は
したがって、となるように、
θをとれば、は応力テンソルの主応力(主値)になる。
また、主応力は、次のように、行列(テンソル)の固有方程式を解くことによて求めることができる。
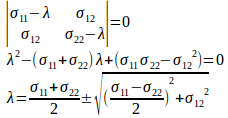
よって、主応力をσ₁、σ₂とすると、
となる。
せん断応力の絶対値が最大になるとき、その
を最大せん断応力(主せん断応力)といい、主応力σ₁、σ₂を用いると、
で与えられる。
問3 σ₁₁=2+√2、σ₂₂=2−√2、σ₁₂=√2のとき、主応力とその方向を求めよ。また、最大せん断応力を求めよ。
【解】
(6)より、
また、主応力は(7)より
よって、(8)より最大せん断応力は
である。
(解答終)
O-x₁x₂に対し角度θだけ傾いている(仮想的な)断面に作用する垂直応力σ'とせん断応力τ'は、この断面の垂直なベクトル、すなわち、法線ベクトル(直交座標系O-x'₁x'₂での成分であることに注意!!)
に、(3)〜(5)で与えられる成分をもつ応力テンソルを作用させることにより、次のように求めることができる。
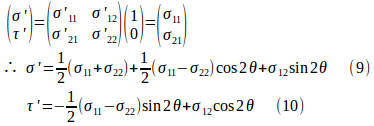
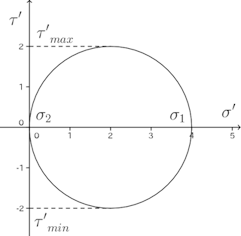
このθを消去すると、
これをモールの応力円という。
となり、これを用いて、主応力、最大せん断応力を求めることもできる。
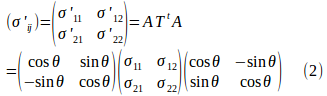




ダイセルの久保田博士が言うようにこれと破壊力学が合体した材料物理数学再武装ってのが結構面白いよね。
by サステナブル風力発電 (2021-11-01 01:30)