第１２回 内分と外分

第１２回　内分と外分

§１　内分

線分AB上に点Pがあり、AP:PB=m:n　（m>0、n>0）となるとき、点Pは線分ABをm:nに内分するといい、点Pを内分点という。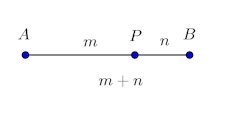

AP:PB=m:nだから、

　　

になる。

あるいは、AP:AB=m:(m+n)になるので

　　

A、B、Pが数直線上のA(a)、B(b)、P(p)という点である。

a<bのとき、

　　

a>bのとき、AP=a−p、PB=p−bになり、この時も

　　

になる。

§２　外分

線分ABの延長線上に点Qがあり、

　　AQ:QB=m:n

となるとき、点Qは線分ABをm:nに外分するという。また、この点QをABの外分点という。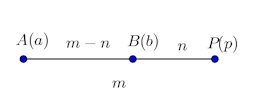

数直線上の点A(a)、B(b)、Q(q)で、a<b、かつ、m>n>0とすると、

　　

になる。

形式的な話になるけれど、

　　

となるので、外分点Qは線分ABをm:−nの内分点と考えることもできる。

そして、

　　

とし、nm>0のとき内分、nm<0のとき外分と考えることもできる。

あくまで形式的議論で、こんなものを覚える必要はない。百害あって一利なしなので、

§３　面積比

三角形の面積Sは底辺BC=a、高さをhとすると

　　

になる。

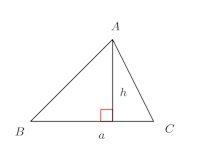
したがって、三角形の面積は、底辺の長さがが一定ならば高さに比例し、高さが一定ならば底辺の長さに比例することがわかる。

だから、２つの三角形の面積比には次の関係があることがわかる。

【１】　２つの三角形の面積の比は、等底ならば高さの比、等高ならば底辺の比に等しい。

【２】　一辺が共通ならば

　　

【１】について、少し説明すると、等底のときは、△ABCと△A'BCの面積比は

　　

となり、２つの三角形の面積比は高さの比になる。

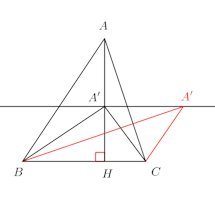
また、高さが一定ならば、△ABDと△ADCの面積比は

　　

となり、三角形の底辺の比AD:BC=m:nになる。

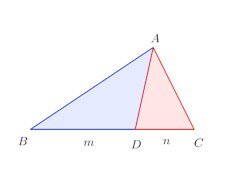
また

　　

という関係がある。

【２】については、次の図を見ると何故こうなるかわかると思う。

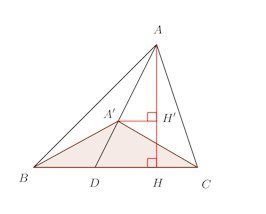
このとき、△ABCと△A'BCの高さの比は

　　H'H:AH=A'D:AD

になるので、

　　

となる。

問題　△ABCの辺BCをm:nに内分する点をDとし、線分ADをp:qに内分する点をA'とする。

次の問いに答えよ。

（１）　△ABCと△A'BCの面積比を求めよ。

（２）　△ABCと△A'BDの面積比を求めよ。

【解】

（１）　△ABCと△A'BCは底辺BCを共通しているので面積比は

　　

である。

（２）　△A'BCと△A'BDは高さが共通。よって、面積比は

　　

①と②をかけると

　　

面積比を求めることができた。

何でこんなことを急にやり出しかというと、初等幾何で有名なメネラウスの定理とチュバの定理の証明をするためです。

タグ：初等幾何