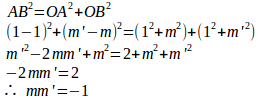第１７回 三平方の定理（ピタゴラスの定理）

第１７回　三平方の定理（ピタゴラスの定理）

§１　三平方の定理

定理　三平方の定理（ピタゴラスの定理）

△ABCにおいて∠C＝∠Rならば

　　

である。

逆も成り立つ。

【証明】
この図が証明。

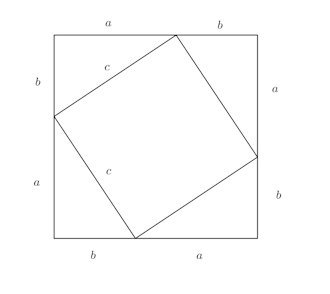
一辺(b+c)の正方形の面積＝４×直角三角形ABCの面積＋一辺cの正方形の面積

　　

（逆の証明）

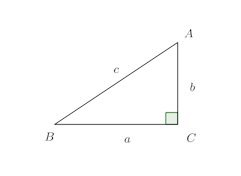
B'C'=a、A'C'=b、∠C'=∠Rである△A'B'C'を考える。直角三角形なので

　　

一方、仮定より△ABCでは

　　

①、②より

　　

c'>0、c>0なので、c'=c。

よって、

　　△ABC≡△A'B'C'　（三辺相等）

したがって、

　　∠C=∠C'=∠R

となり、c²=a²+b²ならば∠C=90°の直角三角形である。

（証明終わり）

三平方の定理の逆の証明では、「同一法」と呼ばれる証明法を用いている。

同一法とは、

「pならばq」が真で、かつ、qを満たすものがただ一つならば、「pならばq」の逆命題「qならばp」が成立する

ということを用いて、逆命題を証明する数学の証明法。

三平方の定理の簡単な証明としては、この他に以下のようなものがあります。

【略証】

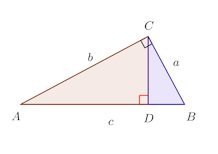
点CからABに垂線をおろし、交点をそのDとする。

△ABC∽△ACDだから

　　

また、△ABC∽△CBDだから

　　

よって、

　　

【略証終わり】

あるいは、面積比は相似比の２乗を使って

　　

そして、△ABC=△ACD＋△CBDだから

　　

と証明してもいいケロ。

中学校の教科書に載っている三平方の定理の証明は難しいので、あの証明は駄目だケロ。

では、問題を。

問題１　２辺が６、８である直角三角形は２通りある。それぞれの３辺で残りの辺の長さを求めよ。

【解】

２辺が直角を挟み、残りの１辺が直角三角形の斜辺である場合と、そうでない場合の２通りがある。

直角三角形の斜辺である場合、

　　

そうでない場合、このとき、c=8になるので、残りの辺の長さxとすると

　　

となる。

問題２　直角三角形ABCで、斜辺BCの中点をMとするとき、線分AMの長さをもとめよ。

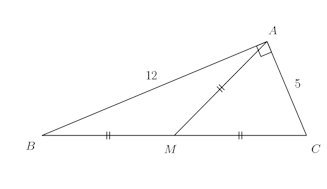
【解】

直角三角形なので、AM=BM=MC。

x=AMとすると、BC=2xになるので、三平方の定理より

　　

問題３　四角形ABCDで、対角線が直交するとき、

　　

であることを証明せよ。

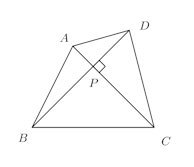
【解】

直角三角形PABで

　　

同様に、

　　

よって、

　　

§２　三平方の定理の平面図形への応用

（１）　座標平面上の２点間の距離

座標平面上にある２点A(x₁,y₁)、B(x₂,y₂)の距離ABは

　　

となる。

これは、これまでに何度も使ってきたけれど、三平方の定理を使って、このように求められる。

問題４　３点A(2,6)、B(−4,2)、C(0,−4)を頂点とする三角形はどのような三角形か。また、その面積を求めよ。

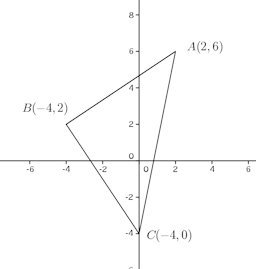
【解】

　　

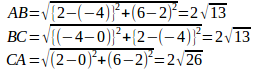
よって、

　　

となり、∠Bが直角の直角二等辺三角形。

面積Sは

　　

（解答終わり）

問題４では

　　

が成立するので、∠B=∠Rの直角三角形。さらに、AB=BC=2√13だから二等辺三角形。このことから∠C=90°、∠A=∠B=45°の直角二等辺三角形であることがわかる。

（２）　直交する直線の傾きの積mm'=−1

y=mx+nとy=m'x+n'という２直線があるとする。この２直線が直交するならば傾きの積mm'=−1であり、傾きの積がmm'=−1ならば直交する。

このことは、中学や高校で習ったと思う。そして、これは三平方の定理を使って簡単に証明することができる。

傾きだけの問題なので、l:y=mx、l':y=m'xとしても一般性は失われないので、議論を簡単にするために、この場合で考えることにする。

　――lとl'との交点が原点Oに一致するように、lとl'を平行移動させたと考えてもいい――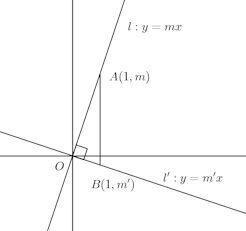

直線l上にA(1,m)、l'上に点B(1,m')をとる。この２直線は原点Oで直交するので、△OABは∠AOB=90°の直角三角形。

よって、三平方の定理が成り立ち

　　

タグ：初等幾何