第２７回 三角形の５心 続き

第２７回　三角形の５心　続き

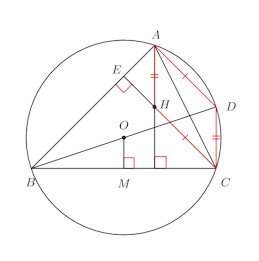
問題１　三角ABCの外心をO、垂心をHとするとき、OよりBCにおろした垂線をOMとすると、

　　

であることを示せ。

【証明】

△ABCの外接円とBOの延長の交点をDとする。

そうすると、

　　AD⊥AB　（直角三角形の中線の長さと斜辺の半分の長さは等しい）

また、Hは△ABCの垂心なのでCHの延長とABは垂直。よって、

　　HC⊥AB

だから、

　　

同様に、

　　AH⊥BC、OM⊥BC

よって、

　　

以上のことから、四角形AHCDは平行四辺形で、

　AH=DC

△BCDに注目。

　　BO=OD

　　BM=MC　（中心Oから弦BCにおろした垂線の足BはBCの中点）

よって、中点連結定理より

　　2OM=DC=AH

（証明終わり）

オイラー線

三角形において、外心をO、重心をG、垂心をHとすると、O、G、Hは一直線上にあり、

　　

【証明】

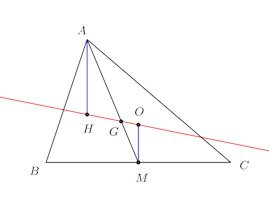
BCの中点をMとする。

Hは内心なので、AH⊥BC。

また、OM⊥BCなので、

　　

問題１より

　　

線OHとAMの交点をGとする。

　　

だから、

　　△AHG∽△MOG

よって、

　　AG:GM=AH:OG=2:1

Gは中線AMを2:1に内分しているので、△ABCの重心である。

よって、外心O、重心G、垂心Hは一直線上にある。

（証明終わり）

この関係は、どんな三角形でも成立するものです。

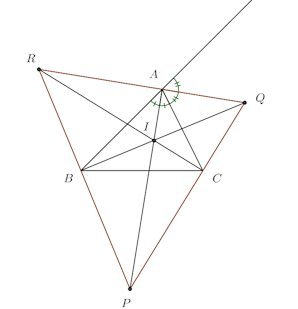
問題２

△ABCの内心をI、３つの傍心をP、Q、Rとすると、Iは△PQRの垂心であることを証明せよ。

【証明」

AI、APは∠BACの２等分線なので、A、I、Pは同一線上に存在する。

同様に、B、I、Q、そして、C、I、Rもそれぞれ１直線上に存在する。

傍心なので、Q、A、R、また、R、B、P、そして、P、C、Qもそれぞれ１直線上に存在する。

で、角関係より

　　

よって、

　　

同様に、

　　

したがって、Iは△PQRの垂心である。

（証明終わり）

タグ：初等幾何