第２９回 円周角の定理

第２９回　円周角の定理

次の２つの定理を既知のものとして話を進めることにする。

定理A

等しい中心角に対する弧または弦は等しい。

定理B（定理Aの逆）

等しい弧または弦に対する中心角は等しい。

では、円周角の定理。

円周角の定理

１つの弧に対する円周角は、その弧に対する円周角の半分に等しい。

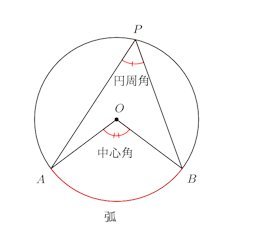
弧ABに対する円周角∠APBは

　　

というわけです。

【円周角の定理の証明】

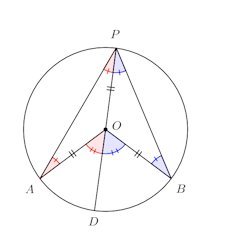
（１）　円の中心Oが直線PAまたは直線PB上にある場合

OがPB上にある場合を証明すれば十分。

△OAPはOP=OAの二等辺三角形。

よって、

　　∠APO=∠OAP

∠AOBは∠APOの外角なので、

　　

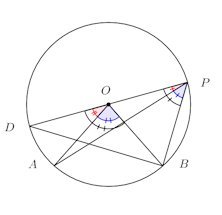
（２）　円の中心Oが∠APBの内部にある場合

POの延長と円Oの交点をDとする。

（１）より

　　

（３）　円の中心Oが∠APBの外部にある場合

（１）より

　　

（１）、（２）、（３）のいずれの場合でも、

　　

である。

（証明終わり）

この円周角の定理と、定理A、Bから次のことが言える。

定理　同じ円、または、半径の等しい円において

（１）　等しい弧に対する円周角は等しい

（２）　等しい円周角に対する弧は等しい

等しい弧ならば、中心角は等しく、円周角は中心角の半分に等しいので、円周角は等しくなる。

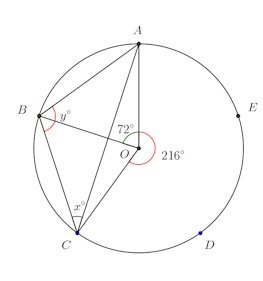
また、等しい円周角ならば、中心角は等しく、したがって、弧も等しくなる、からだケロ。

問題１　円周を５等分する点を順に、A、B、C、D、Eとする。∠ACB、∠ABCを求めよ。

【解】

円周を５等分するので、弧ABの中心角∠AOBは

　　

よって、円周角の定理より∠ACBは

　　

円周角∠ABCに対応する弧は弧CDEAで、これに対する中心角∠COAは

　　

よって、円周角の定理より

　　

問題２　弧AM=弧MB、弧AN=弧NCであれば、△ADEは２等辺三角形であることを証明せよ。

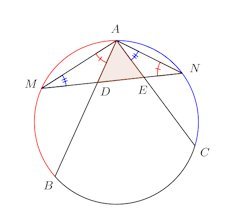
【証明】

等しい弧に対する円周角は等しい。

弧AM=弧MBだから

　　

弧AN=弧NCだから

　　

で、三角形の内角と外角の関係より

　　

よって、△ADEは２等辺三角形である。

（証明終わり）

問題３（方べきの定理）

円の２つの弦AB、CDの交点をPとするとき、

　　

であることを示せ。

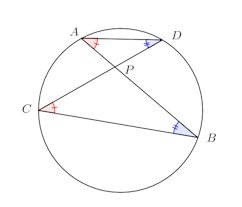
【証明】

弧ACの円周角なので、円周角の定理より

　　∠ABC=∠ADC

弧BDの円周角なので

　　∠BCD=∠BAD

よって、

　　△APD∽△CPB

△APDと△CPBは相似なので

　　

（証明終わり）

方べきの定理は、これからいろいろなところで使うので、憶えておくと便利です。

タグ：初等幾何