第２９回 円周角の定理の逆

第２９回　円周角の定理の逆

円周角の定理の逆を取り上げる前に、復習として、円周角の定理。

円周角の定理

１つの弧に対する円周角は、その弧に対する円周角の半分に等しい。

そして、円周角と孤に関する次の定理。

定理

同じ円、または、半径の等しい円において

（１）　等しい弧に対する円周角は等しい

（２）　等しい円周角に対する弧は等しい

では、今回の本題である円周角の定理の逆を紹介します。

円周角の定理の逆

２点P、Qが直線A、Bに関して同じ側にあるとき、

　　∠APB=∠AQB

ならば、４点A、B、P、Qは同じ円周上にある。

この定理を証明する前に、まず、次のことを証明します。

補題

円周上に３点、A、B、Cがあり、直線ABに関してCと同じ側にPをとるとき

（ⅰ）　点Pが円周上にあるとき　∠APB=∠ACB

（ⅱ）　点Pが円の内部にあるとき　∠APB>∠ACB

（ⅲ）　点Pが円の外部にあるとき　∠APB＜∠ACP

である。

【証明】

（ⅰ）　Pが円周上にあるとき、円周角の定理より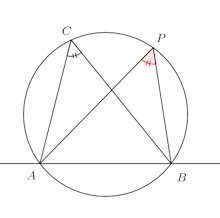

　　∠APB=∠ACB

（ⅱ）　Pが円の内部にあるとする。APの延長と円の交点をQとする。

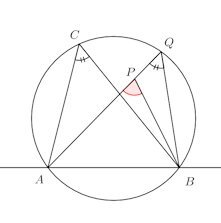
∠APBは△PBQにおける∠BPQの外角なので

　　∠APB=∠AQB+∠PBQ>∠AQB

また、円周角の定理より

　　∠AQB=∠ACB

よって、

　　∠APB>∠ACB

である。

（ⅲ）　Pが円の外側にあるとする。APと円の交点をQとする。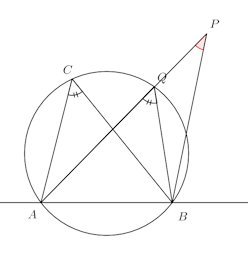

∠AQBは△BPQの∠BQPの外角なので

　　 ∠AQB=∠APB+∠PBQ>∠APB

また、円周角の定理より

　　∠AQB=∠ACB

よって、

　　∠APB<∠AQB

（証明終わり）

 

定理　（円周角の定理の逆）

２点P、Qが直線A、Bに関して同じ側にあるとき、

　　∠APB=∠AQB

ならば、４点A、B、P、Qは同じ円周上にある。

【証明】

（ⅰ）、（ⅱ）、（ⅲ）の条件はすべてを尽くしており、また、（ⅰ）、（ⅱ）、（ⅲ）の結論はそれぞれ両立しない。

よって、転換法によって、この命題は真である。

（証明終わり）

 

例１

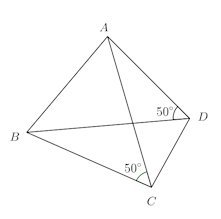
直線ABに関して点C、Dは同じ側にあり、

　　∠ACB=∠ADB=50°

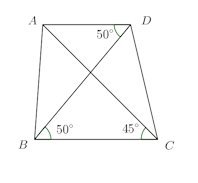
だから、円周角の定理の逆によって、点A、B、C、Dは同一円周上にあり、四角形ABCDはこの円に内接する。

例２

直線ABに関してC、Dは同じ側にあるけれど、

　　∠ACB≠∠ABD

だから、点A、B、C、Dは同一円周上にない。

 

問題

図のように、△ABCの辺ABを１辺とする正三角形ADB、辺ACを１辺にする正三角形ACEがある。

（１）　△ABE≡△ADCであることを示せ。

（２）　４点A、D、B、Pが同一円周上にあることを示せ。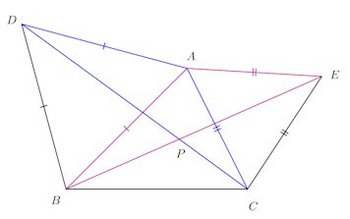

【証明】

（１）△ADBは正三角形なので

　　AB＝AD

△ACEは正三角形なので

　　AE＝AC

また、

　　
２辺挟角相等より

　　△ABE≡△ADC

（２）　点A、Pを直線で結ぶ。

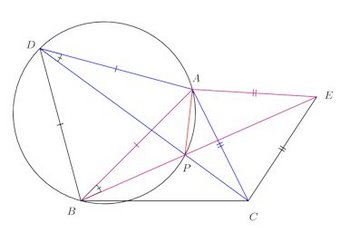
△ABE≡△ADCより、

　　∠ADP=∠ABP

また、点D、Pは直線APに関して同じ側にある。

よって、円周角の定理の逆より

４点A、D、B、Pが同一円周上にある

（証明終わり）

タグ：初等幾何