番外編 数学的帰納法を使って、相加平均≧相乗平均≧調和平均

番外編　数学的帰納法を使って、相加平均≧相乗平均≧調和平均を！！

問題１　次の不等式を証明せよ。ただし、文字はすべて正の数である。

　　

相加平均≧相乗平均を使っていいというのならば、

　　

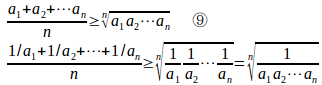
が成立するので、

　　

とすぐに証明できる。

しかし、大学入試でこのような証明が許されるのかといえば、駄目だろうね(^^)

だから、この問題の場合は、次のように数学的帰納法を使って証明すべきなのだろう。

【証明】

（Ⅰ）　n=1のとき

　　

よって、n=1のとき、①は成立する。
（Ⅱ）　n=kのとき

　　

が成立すると仮定する。
（Ⅲ）　n=k+1のとき
　　

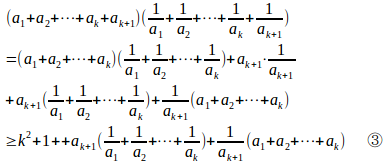
ここで、

　　

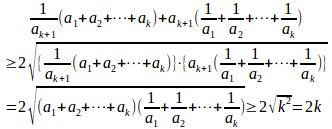
この結果を③に代入すると

　　

となり、n=k+1のときにも成立する。

数学的帰納法より、すべての自然数nについて

　　

である。

（証明終わり）

この不等式を使うと、

　　

や

　　

という不等式を作ることができる。

問題２　を正の数とする。

（１）　x>0のとき、次の関数の最小値を求めよ。

　　

（２）　上の結果を用いて、数学帰納法によって、次の不等式を証明せよ。

　　

【解】

（１）　f(x)を微分する。

　　

とおくと、x<αではf'(x)<0、x>αでf'(x)>0なので、x=αのときf(x)は最小。

よって

　　

（２）　n=1のとき、だから、成立。

n=kのとき

　　

と仮定する。

（１）の結果より、x>0ではf(x)≧f(α)

　　

、を上の式に代入すると、

　　

となり、n=k+1の時にも成立する。

よって、数学的帰納法により、すべての自然数nに対して

　　

である。

（解答終わり）

そして、この結果を使うと、

　　

この逆数をとると、

　　

この左辺は調和平均と言われるもので、このことから、調和平均≦相乗平均≦相加平均であることがわかる。

で、問題１に戻って

　　

！！

タグ：微分積分