第３９回 軌跡のイントロ

第３９回　軌跡のイントロ

軌跡とは、ある条件を満たす点の集まり、点の集合のこと。

では、問題。

問題１　座標平面上２定点A₁(−a,0)、A₂(a,0)がある。この平面上において

　　

をみたす点Pの全体が作る図形の方程式を求めよ。ただし、a>0である。

【解】

　　

点Pの座標を(x,y)とすると

　　

よって、

　　

したがって、(5a/3,0)を中心とする半径4a/3の円である。

（解答終わり）

このようにして得られる円をアポロニウスの円という。

では、A₁P=A₂Pのときはどうなるか。

　　

だから

　　

で、x=0というのは、A₁(−a,0)とA₂(a,0)の垂直二等分線。

ということで、

　　

を満たす点Pは、どうやら、

　　m≠nのとき　アポロニウスの円

　　m=nのとき　A₁(−a,0)とA₂(a,0)の垂直二等分線

になりそうだ。

ということで、次の問題。

問題２　m、nが正の数で

　　

のとき、次のことを示し、その図形的な意味を説明せよ。

m≠nのとき

　　

m=nのとき

　　

ただし、 はの内積をあらわす。

ベクトルの内積は、２つのベクトルのなす角度をθとすると

　　

だにゃ。

【解】

m≠nのとき

　　

とし、さらに

　　

としとすると、点CとDは、それぞれ、線分ABをm:nに内分する点と外分する点をあらわしている。

そして、

　　

は、点PがABのm:nの内分点Cと外分点Dを両端とする円周上に存在することを意味する。

m=nのとき

　　

これは、点Pが線分ABの垂直２等分線上に存在することを意味する。

（解答終わり）

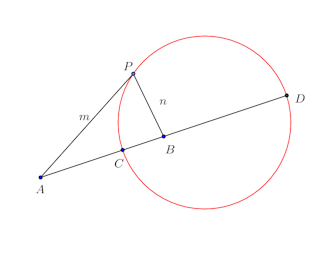
４点A、C、B、Dがこの順にならび同一線上にあるとする。このとき、

　　AC:CB=AD:DB

が成り立つとき調和点列という。

そして、上の問題の証明からアポロニウスの円と調和点列は深い関係があり、

　　

という関係があるのであった。

タグ：初等幾何 ベクトル