ベクトル 空間ベクトルの内積と成分

ベクトル　空間ベクトルの内積と成分

§　空間ベクトルの内積の成分表示

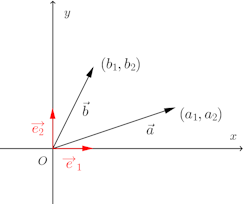
空間では、ベクトルは次のように３つの成分で表される。

　　

基本ベクトルを用いて表すと

　　

したがって、との内積は

　　

となり、

　　

になる。

何故ならば、

　　

だから。

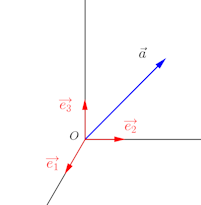
§　方向余弦

x軸、y軸、z軸の正の向きとベクトルのなす角を、それぞれ、α、β、γとすると

　　

となり、同様に

　　

となる。

また、

　　

だから、

　　

この３つの組をの方向余弦といい、

　　

であらわす。

のとき

　　

したがって、方向余弦には次の関係がある。

　　

§　問題編

ベクトルのなす角θ

　　

問題１　のなす角θ（0°≦θ≦180°）を求めよ。

【解】

　　

また、

　　

よって

　　

よって、θ=30°

（解答終わり）

問題２　のとき

（１）　ベクトルのなす角を求めよ。

（２）　の両方に垂直な単位ベクトルを求めよ。

【解】

（１）　、また

よって

　　

よって、θ=60°。

（２）　の両方に垂直な単位ベクトルをとする。

単位ベクトルなので

　　

はに垂直なので

　　

これを代入すると

　　

よって、

　　

（解答終わり）

問題３　大きさが２、x軸、y軸の正の向きとなす角がそれぞれ45°、60°であるベクトルの成分を求めよ。、また、そのベクトルがz軸の正の向きとなす角度を求めよ。

【解】

求めるベクトルの方向余弦をl、m、nとすると

　　

よって
　　

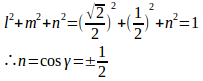
したがって、γ=60°、120°。

求めるべきベクトルをとすると

　　

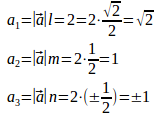
よって、(√2,1,1)または(√2,1,−1)。

（解答終わり）

問題３から分かるように、一般にベクトルがx軸、y軸、z軸の生の向きとなす角α、β、γの和α+β+γは、一般に180°にならないので、注意して欲しいにゃ。

タグ：ベクトル

ベクトル 内積と成分（平面の場合）

ベクトル　内積と成分（平面の場合）

平面上にある２つのベクトルの内積の成分表示を求めることにする。

平面上ではベクトルの成分は

　　

であり、基本ベクトルをとすると、それぞれ

　　

となる。

したがって、内積は

　　

また基本ベクトルは大きさが１で互いに直交するので、

　　

この結果を上式に代入すると

　　

特に、と基本ベクトルとの内積は
　　

つまり、ベクトルの成分はベクトルと基本ベクトルとの内積になっている。

問題１　のなす角θ（0≦θ≦180°）を求めよ。

【解】

内積の定義は

　　

よって、

　　

内積を求めると

　　

また、

　　

よって、
　　

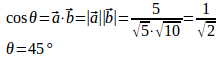
問題２　ベクトルに垂直で、大きさがに等しいベクトルを求めよ。

【解】

　　とする。

だから

　　

だから

　　

よって、

　　

これを解くと(x,y)=(3,−4)、(−3,4)。

よって

　　

問題３　３点A(−1,0)、B(0,2)、C(−3,1)が与えられている。

　　
を満たす第１象限の点Dの座標を求めよ。

【解】

点Dの座標を(x,y)とする。

　　

よって、

　　

これを解くと、(x,y)=(2,1),(-2,3)。

Dは第１象限の点なので、D(2,1)。

問題４　ベクトルに対して、ベクトルの成分を、次のそれぞれの場合について求めよ。

（１）　とが平行の場合

（２）　とが垂直の場合

【解】

（１）　とが平行なのでを満たす実数kが存在しなければならない。

よって

　　

また、であり、b=−2

（２）　だからでなければならない。

よって

　　

また、のとき

　　

であり、よって、b=2である。

 

タグ：ベクトル