ベクトル 内積の不等式への応用

ベクトル　内積の不等式への応用

成分で表される２つの平面ベクトルがあるとき、その内積は

　　

になる。

空間ベクトルの場合、つまり、のとき、この内積は

　　

になる。

では、問題。

問題１　ベクトルの内積を利用して、次の不等式を証明せよ。

　　

【証明】

とし、この２つのベクトルのなす角度をθとする。

　　

また

　　

よって、

　　

等号が成立するのはcos²=1、または、またはのとき。

cos²θ=1になるのはθ=0またはθ=180°のときで、これは。

よって、等号成立は、またはまたはのときである。

（証明終わり）

また、

　　

は一般に成り立つので、とすれば、次の不等式が得られる。

　　

これを使って、次の問題を解くことにする。

問題２　x、y、zが負でない実数でx+2y+3y=1のとき

　　

の最大値を求めよ。

【解】

　　

等号が成立するのは、

　　

よって、

　　

（解答終わり）

こうした解法がいいかどうかは別にして、こういうふうに解くことができる。

次の問題は有名問題なので、やらないわけにはいかない。

問題３　零ベクトルでない２つのベクトルが与えられている。

が最小となるとき

（１）　tの値を求めよ。

（２）　とが直交することを示せ。

【解】

（１）　だから２乗しても大小関係は変わらない。だから、を２乗する。

　　

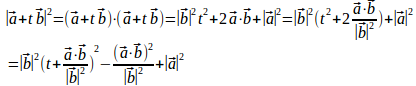
よって、

　　

の時に最小。

（２）

よって、とが直交する。

（解答終わり）

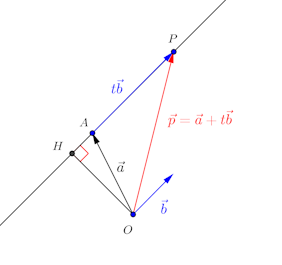
とすると、点Pはで表される点Aを通り、に平行な直線上の点。
は、原点Oと点Pとの距離。

だから、問題３の（１）で、原点Oと直線上の点との距離の最小値を求めていることになる。

原点Oからこの直線におろした垂線の足をHとすると、（２）では、直線と原点との距離が最小のとき、OHと直線が直交しているということを表している。

タグ：ベクトル