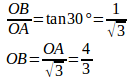ワンポイントゼミ１ 定積分と面積

ワンポイントゼミ１

問題　放物線がある。次の問いに答えよ。

（１）　x=1における、この放物線の接線の方程式を求めよ。

（２）　放物線と（１）で求めたこの放物線の接線と、x軸、y軸で囲まれた斜線で示された領域の面積を求めよ。

y=f(x)のx=aにおける接線の方程式は

　　

y'=f’(x)=−xだから、x=1における接線の方程式は

　　

これが（１）の答えになる。

これから、接線の方程式とx軸との交点Aのx座標（x切片）は5/2、y軸との交点Bのy座標（y切片）も5/2であることがわかる。

求める斜線部の面積は、△OABの面積からピンク色で示された領域の面積を引いたもの。

△OABの面積は

　　

ピンク色の領域の面積は

　　

したがって、求める面積は

　　

このように計算をしてもよい。

もちろん、

　　

として求めてもよい。

タグ：微分積分

体積の問題１

体積の問題１

回転体の体積

（１）　曲線y=f(x)（a≦x≦b）をx軸のまわりに回転したとき

　　

（２）　曲線x=g(y)（c≦y≦d）をy軸のまわりに回転したとき

　　

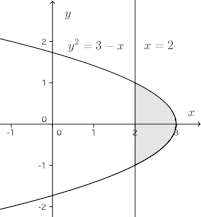
問題１　曲線y²=3−xと直線x=2とで囲まれた部分を、x軸のまわりに回転してできる図形の体積を求めよ。

【解】

y²=3−xとx=2の交点のy座標は

　　

求める体積Vは、

　　

とすると、

　　

（解答終わり）

なお、上の計算では、y⁴−6y²+5が偶関数だから

　　

を使っている。

 

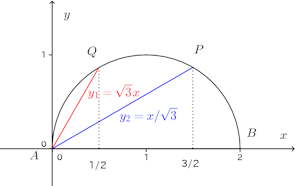
問題２　図は半径１の半円で、弦AP、AQの直径ABとなす角はそれぞれ30°、60°である。弦AP、AQと弧BPを囲む部分を直径ABのまわりに１回転してできる立体の体積を求めよ。

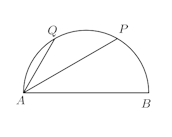
【解】

Aを原点に、ABをx軸にとると、円の方程式は

　　

また、直線APと直線AQの方程式は

　　

よって、求める体積Vは

　　

（解答終わり）

問題３　次の曲線をy軸のまわりに回転してできる立体の体積を求めよ。

　　

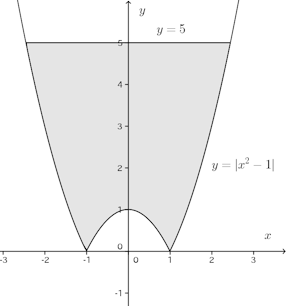
【解】

　　

求める体積Vは

　　

とすると、曲線x₁をy軸周りに回転してできる立体の体積から曲線x₂をy軸まわりに回転してできる立体の体積を引いたものと等しい。

　　

（解答終わり）

 

問題４　曲線y=2x−x²と直線y=−xとで囲まれた部分をx軸のまわりに回転してできる回転体の体積を求めよ。

【解】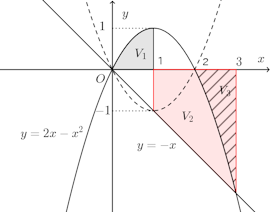

y=2x−x²とx=1とx軸とで囲まれた部分をx軸のまわりに回転してできる立体の体積をV₁（図中の灰色の部分）、y=−xとx=1、x=3とx軸で囲まれた部分をx軸まわりに回転してできる立体の体積をV₂（ピンクの部分）、y=2x−x²とx=2、x=3とx軸で囲まれた部分をx軸まわりに回転してできる立体の体積をV₃（斜線部）とする。

求める体積Vは

　　

である。

　　

したがって、

　　

（解答終わり）

タグ：微分積分

何でも、微分積分を使えばいいというものではない

何でも、微分積分を使えばいいというものではない

問題

原点を中心とする半径２の４分円Cがある。半径OPとx軸のなす角が60°であるC上の点Pにおける接線とx軸、y軸との交点を、それぞれ、A、Bとする。

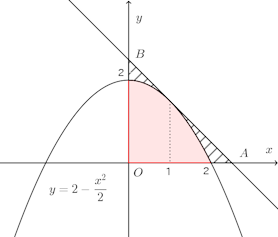
図中には、直線ABと４分円C、x軸、y軸とで囲まれた領域を斜線で示してある。

（１）　斜線部の面積を求めよ。

（２）　斜線部をx軸のまわりに回転させてできる立体の体積を求めよ。

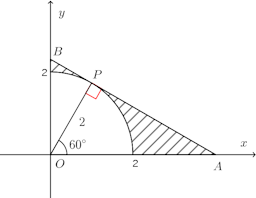
ねこ騙し数学では、現在、微分積分の問題演習をやっているので、おそらく、多くの人はこの問題を微分積分を使ってとこうとするに違いない。

しかし、それは、まさしく、「牛刀をもって鶏を割く」である。

この問題は、微分積分を使わず中学３年生程度の数学の知識だけで簡単に解けてしまう問題であって、そもそも、微分積分を使う必要がないのだ。

積分を使って解こうとすると、

（１）　点Pの座標は(1,√3)だから、接線ABの方程式は

　　

よって、Aのx座標は4。

したがって、求めるべき面積は

　　

という積分の計算をしなければならなくなる。

　　

を求めるためには、三角関数の微分、置換積分の知識が必要で、現在やっている問題演習の範囲を逸脱してしまう。

もっとも、この積分は半径２の４分円の面積になるので、π×2²÷4=πになることがすぐにわかる。

このような図形的な解答をするのであるならば、

①より、Bのy座標は4/√3だから、

　　

よって、求めるべき面積は

　　

こうすれば、
先に述べたように、積分の計算は一切、不要である。

何でもかんでも微分積分を使えばいいというものではない！！

いやいや、最初から、次のように解くべきだ。

求めるべき面積は、△OABの面積から半径２の４分円の面積を引いたもの。

点Pの座標は(1,√3)だから、接線ABの方程式は

　　

よって、Aのx座標は4、Bのy座標は4/√3。

したがって、

　　

点Pの座標は

　　

点Pにおける接線の方程式①を求めるにあたって、

円：x²+y²=r²の円周上の点(x₀,y₀)における接線の方程式は

　　

を使っている。

実は、この問題、接線の方程式すら求める必要がない。
∠OAP=30°だから、

　　

また、

　　

（２）は、積分を使うと、

　　

この計算をすれば、答えが出てくる。

しかし、この問題も図形的な考察から、次のように簡単に解けてしまいます。

求めるべき体積は、△ABOをx軸のまわりに回転してできる円すいの体積から半径２の４分円をx軸のまわりにできる半球の体積を引いたもの。

したがって、

　　

タグ：微分積分

体積

体積

§１　一般の立体の体積

立体をx軸に垂直な平面で切ったときの断面積がxの関数S(x)であるとき、この立体のx=aとx=bとの間の体積Vは

　　

である。

例　底面積A、高さhの角すいの体積

角すいの頂点を原点Oに、Oから底面におろした垂線をx軸にとる。すると、x軸に垂直な平面が角すいを切り取る断面積S(x)は

　　

したがって、

　　

問題１　底面の半径がaであるような直円柱がある。底面の直径を通り、底面と４５°の角をなす平面でこの直円直円柱を切り、この平面と底面および側面で囲まれた立体を作る。この立体の体積を求めよ。

【解】

底面の中心をOとし、底面の直径をx軸にとる。

x座標がxである点をとおりx軸に垂直な平面によって切り取られる立体の断面は、直角２等辺三角形で、その断面積S(x)は

　　

したがって、求める体積は

　　

（解答終わり）

 

§２　回転体の体積

（１）　曲線y=f(x)（a≦x≦b）とx軸とで囲まれた部分をx軸のまわりで回転してできる立体の体積

　　

（２）　曲線x=g(y)（c≦y≦d）とy軸とで囲まれた部分をy軸のまわりで回転してっできる立体の体積は

　　

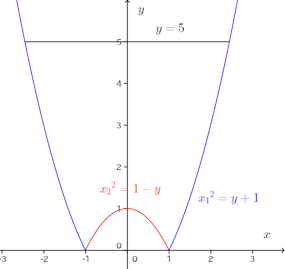
問題２　曲線y=1−x²とx軸で囲まれた図形が、x軸のまわりを回転してできる立体の体積をV₁、y軸のまわりを回転してできる立体の体積をV₂を求めよ。

【解】

回転させる図形は次の通り。

　　

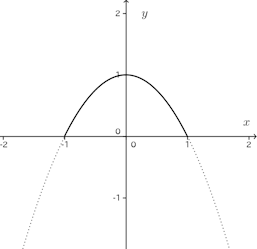
したがって、x軸のまわりで回転させて得られる図形の体積V₁は
　　

y軸のまわりで回転させて得られる図形の体積V₂は

　　

（解答終わり）

 

（３）　２つの曲線y=f(x)、y=g(x)（f(x)≧g(x)≧0,

a≦x≦b）で囲まれた部分をx軸のまわりに回転してできる回転体の体積Vは

　　

問題３　放物線y=x²−4x+5と直線y=2xとで囲まれた図形をx軸のまわりに回転してできる立体の体積を求めよ。

【解】

y=x²−4x+5とy=2xの交点のx座標は、x=1、x=5。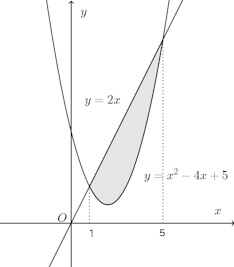

したがって、求める体積Vは

　　

（解答終わり）

 

タグ：微分積分

定積分と面積の問題２

定積分と面積の問題２

問題１　放物線y=x²上の任意の２点P、Qにおける接線の交点をRとするとき、P、Qの位置に関係なく、放物線は△PQRの面積を2:1に分けることを示せ。

【解】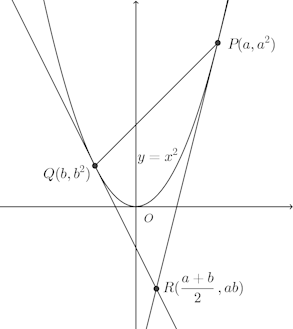

P(a,a²)、Q(b,b²)とすると、P、Qにおける接線の方程式は

　　

よって、交点Rは

　　

直線PQの方程式は

　　

△PQRの面積Sは

　　

直線PQと放物線y=x²で囲まれた図形の面積S₁は

　　

放物線y=x²と２つの接線とで囲まれた図形の面積をS₂とすると

　　

よって、S₁:S₂=1:2で、放物線は△PQRの面積を2:1に分ける。

（解答終わり）

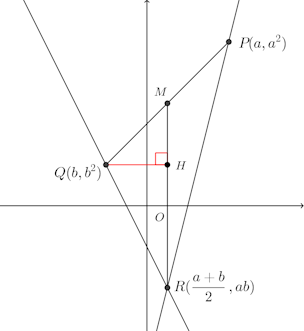
△PARの面積は、PQの中点をMとすると

　　

になるので、線分RMの長さは

　　

△MQRの高さQHは

　　

で、

　　

同様に、

　　

したがって、

　　

と、積分をすることなく簡単に求めることができる。

積分でこの面積を求めるのならば、

　　

を計算すればよい。

また、
　　

の計算では、

　　

という公式（？）を用いている。

問題２　直線y=xと放物線y=x²−xとが囲む面積がy=ax（a>0）で２等分されるようにaの値を定めよ。

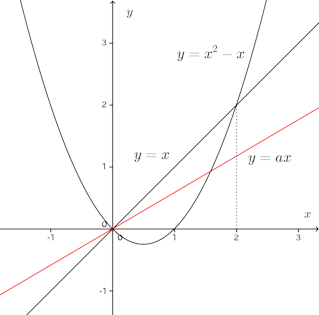
【解】

直線y=xと放物線y=x²−xとが囲む面積Sは

　　

y=axと放物線y=x²−xの交点のx座標を求めると、

　　

だから、y=axと放物線y=x²−xが囲む面積S₁
　　

条件より2S₁=Sだから

　　

（解答終わり）

 

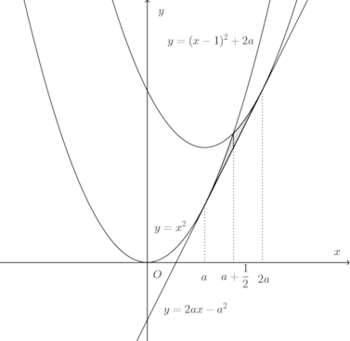
問題３　２つの放物線y=x²、y=(x−1)²+2aがある。

（１）　これらの共通接線の方程式とその接点の座標を求めよ。

（２）　これら２つの放物線と共通接線とで囲まれる部分の面積を求めよ。

【解】

（１）　y=x²上の点(α,α²)における接線の方程式は

　　

これが放物線y=(x−1)²+2aと接する。

よって、次の２次方程式

　　

は重根をもつ。この２次方程式の判別式をDとすると

　　

a=αのとき

　　

よって、共通接線は

　　

接点は、(a,a²)、(a+1,a²+2a)である。

（２）　放物線y=x²、y=(x−1)²+2aの交点のx座標を求めると、x=a+1/2だから、求める面積は

　　　　

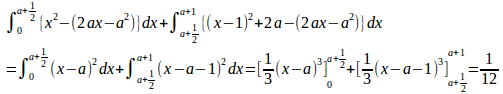
（解答終わり）

問題４　0≦a≦2のとき、y=x²(x−2)とy=ax(x−2)とで囲まれる部分の面積の最大値と最小値を求めよ。

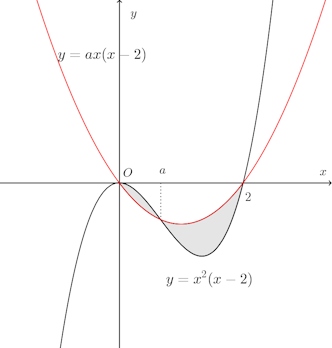
【解】

２つの曲線の交点のx座標は

 　　

よって、x=0,a,2である。

面積S(a)とすると

　　

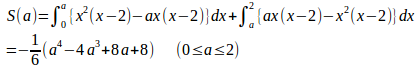
よって

　　

0≦a≦2では、

　　

だから、S(a)の増減表は

a	0	…	1	…	2
S'(a)		−	0	+
S(a)	4/3	減少	1/2	増加	4/3

よって、

a=1/2のとき最小で最小値は1/2

a=0、2のとき最大で最大値は4/3

（解答終わり）

タグ：微分積分

接線の方程式ミニ（おさらい）

接線の方程式ミニ（おさらい）

定積分を使った曲線y=f(x)が囲む領域の面積・体積を求める問題に多数、その曲線y=f(x)の接線絡みの問題が多数出てきますが、

曲線y=f(x)の、この曲線上の点P(a,f(a))における接線の方程式が

　　

であることをよもや忘れていませんよね。

このことを知っていることを前提で話をしているので、これを知らないと、何をやっているかわからなくなってしまう。

例えば、放物線y=f(x)=x²の点P(1,1)における接線の方程式は、y'=f'(x)=2xだから、x=1における微分係数（これは接線の傾き）f'(1)=2×1=2。

したがって、接線の方程式は

　　

になる。

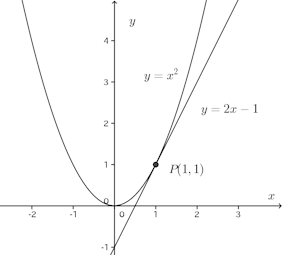
逆に、y=f(x)=x²に接する点A(0,−1)を通過する直線の方程式を求めるには、次のように解けばいい。

【解】接点を(a,a²)とすると、接線の方程式は

　　

この直線が点(0,−1)を通るから

　　

したがって、接点は(−1,1)と(1,1)で、その点における接線の方程式は、②より

　　

である。

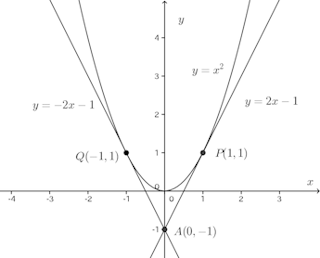
（解答終わり）

微分法を使えば上のような解答になるけれど、f(x)が２次関数の場合は次のように解くこともできる。

【別解】

求める接線は点A(0,−1)を通るので、その傾きをmとすると

　　

③とy=x²の共有点（この場合は接点）のx座標は

　　

の解である。

接点だから、④の解は重複解（重解）でなければならない。

したがって、④の判別式をDとすると、D=0

　　

③より、求めるべき接線の方程式は

　　

接点のx座標は、④より、

m=−1のとき

　　

このときのy座標は

　　

したがって、接点は(−1,1)。

m=1のときは、同様に、(1,1)。

（解答終わり）

タグ：微分積分

定積分と面積の問題１

定積分と面積の問題１

問題１　曲線y=x³−4xと、その上の１点(1,−3)における接線とが囲む図形の面積を求めよ。

【解】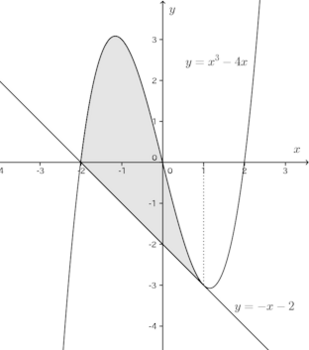

y'=3x²−4だから、点(1,−3)における接線の方程式は

　　

y=x³−4xとy=−x−2との交点を求める。

　　

よって、求める面積は

　　

（解答終わり）

 

問題２　３次関数f(x)がある。f(x)はx=−1およびx=2で極大または極小となり、曲線y=f(x)上の点(0,1)における接線の方程式は3x−2y+2=0である。この曲線と接線で囲まれる図形の面積を求めよ。

【解】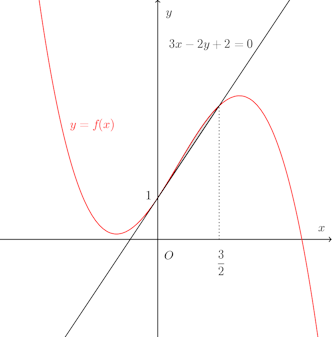

３次関数f(x)はx=−1とx=2で極値を取るので

　　

よって、

　　

この曲線は点(0,1)を通るので

　　

また、点(0,1)における接線は3x−2y+2=0で、接線の傾きが3/2だから

　　

y=f(x)と3x−2y+2=0の交点のx座標はx=0,3/2だから

　　

（解答終わり）

 

問題３　放物線y=x²+x+1と、原点からこの放物線に引いた２本の接線とで囲まれる部分の面積を求めよ。

【解】

原点から放物線に引いて接点を(a,a²+a+1)とすると、接線の方程式は

　　

原点を通るので

　　

よって、接線の方程式は、y=2x、y=−x。

したがって、求める面積Sは

　　

（解答終わり）

 

問題４　（１）　y=x³に３本の接線が引けるP(a,b)の存在する範囲を図示せよ。

（２）　（１）で求めた範囲でx²+y²≦2を満たす部分の面積を求めよ。

【解】

（１）　接点を(t,t³)とすると、接線の方程式は

　　

点P(a,b)を通るので

　　

f(t)=2t³−3at²+bとおくと

　　

よって、f(t)はt=0、t=aで極値をもつ。

f(t)=0が３つの実根をもつ条件は極大値×極小値<0だから

　　

P(a,b)の存在領域は次のとおり。


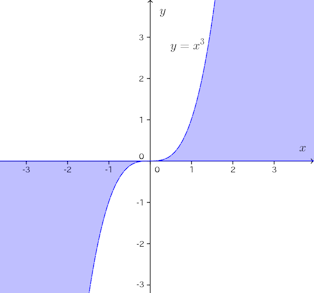
（y=x³とx軸は含まない）。

（２）　求める面積は、図に示す扇型OABの面積から灰色の面積を引いたものを２倍したもの。

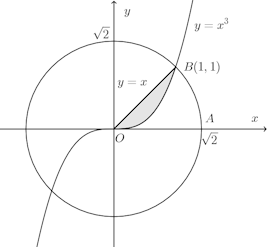
灰色の部分の面積は

　　

扇型OABの面積はπ/4だから、

求める面積は
　　

タグ：微分積分

偶関数と奇関数の積分

偶関数と奇関数の積分

偶関数とは、f(−x)=f(x)が成立する関数のことで、y軸に関して対称な関数。

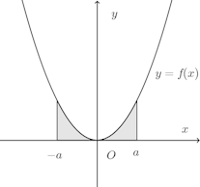
だから、

　　

が成立する。

たとえば、f(x)=x²がその代表的な例であり、

　　

になる。

対して奇関数は、f(−x)=f(x)である関数のことで、これは原点に関して対称である。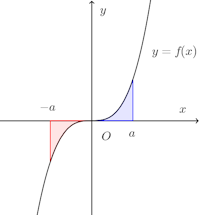

だから、

　　

である。

f(x)=x³がその代表的な例で、

　　

となる。

このことは、上の図を見れば、幾何学的に明らか。

0≦x≦aでf(x)≧0であるとき、

図の中で青で塗られている部分の面積S₁は

　　

赤の部分の面積S₂は

　　

赤で示されている領域は、青で示されている領域を原点を中心にして180°回転させたものだからS₂=S₁で、それゆえに

　　

である。

ということで、例えば、f(x)=x⁴+x³+x²+x+1の場合、

　　

g(x)=x⁴+x²+1、h(x)=x³+xとすると、g(−x)=g(x)だから偶関数、そして、h(−x)=−h(x)だから奇関数。

したがって、

　　

となるので、

　　

と、関数の偶奇性を使って、定積分の計算の省力化をはかることができる。

今やっているのは整関数だけれども、この性質は一般に成立する。

たとえば、

　　

という関数があるとする。

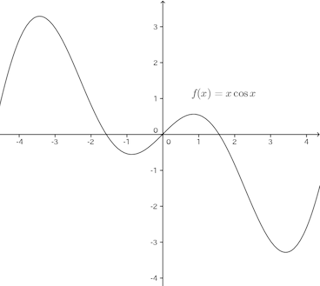
これは図から明らかなように、奇関数なので、計算をするまでもなく、

　　

であることがわかる。

（定）積分では、この性質をよく使うので、知っておくと何かと重宝する。

タグ：微分積分

定積分と面積

定積分と面積

§１　定積分と面積

閉区間[a,b]で関数f(x)が連続、かつ、f(x)≧0であるとする。このとき、曲線y=f(x)とx軸およびx=a、x=bで囲まれた図形の面積をSとするとき、

　　

である。

閉区間[a,b]内の任意の点xをとり、区間[a,x]で曲線とx軸とで囲まれた部分の面積をS(x)とすると、S(x)はxに応じて定まる関数である。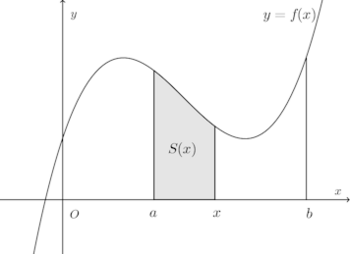

xの増分をΔxに対するS(x)の増分をΔSとすれば、

Δx>0のとき、

　　

Δx<0のとき

　　

である。閉区間[x,s+Δx]のf(x)の最大値、最小値をM、mとする。

Δx>0のとき

　　

Δx<0のとき

　　

であるから、Δxの正負にかかわらず

　　

である。

f(x)は連続だから、Δx→0のとき、m→f(x)、M→f(x)。

したがって、

　　

よって、S(x)はf(x)の不定積分の一つである。

f(x)の不定積分の一つをF(x)とすると、

　　

S(a)=0だから

　　

したがって、

　　

である。

[a,b]で囲まれた面積SはS(b)に等しい。

　　

これを関数f(x)のaからbまでの定積分といい、

　　

であらわし、a、bをそれぞれこの積分の下端、上端という。

問　次のことを証明せよ。

（１）　f(x)が偶関数ならば

　　

（２）　f(x)が奇関数ならば

　　

【解】

（１）　f(x)が偶関数ならば、f(−x)=f(x)で、y=f(x)のグラフはy軸に関して対称。

したがって、

　　

よって、

　　

（２）　f(x)が奇関数であるならば、f(−x)=−f(x)で、y=f(x)のグラフは原点に関して対称。

よって

　　

したがって、
　　

（解答終わり）

 

§２　平面図形の面積

（１）　曲線とx軸とで囲む面積

f(x)は閉区間[a,b]で連続、かつ、f(x)≧0であるとき、y=f(x)とx軸、x=a、x=bで囲まれた面積Sは

　　

である。

[a,b]でf(x)≦0のとき、曲線y=f(x)とx軸、x=a、x=bで囲まれた面積Sは、y=f(x)とx軸に関して対称なy=−f(x)とx軸、x=a、x=bで囲まれた面積に囲まれ面積に等しいから

　　

また、[a,c]でf(x)≧0、[c,b]でf(x)≦0のとき

　　

以上をまとめて

　　

である。

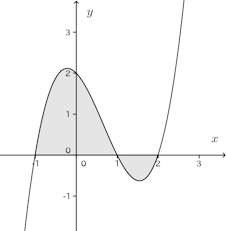
問　曲線y=x³−2x²−x+2とx軸とで囲まれた面積を求めよ。

【解】

　　

したがって、この曲線のグラフは次のようになる。

よって、求める面積は

　　

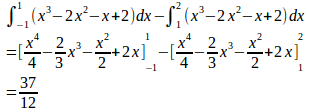
（解答終わり）

求める面積は

　　

ではなく、

　　

であることに注意！！

また、偶関数・奇関数の積分の性質を使って

　　

とすると、計算がすこし楽になる。

（２）　２つの曲線の囲む面積

２つの曲線y=f(x)、y=g(x)と直線x=a、x=bで囲まれた面積は、[a,b]でf(x)≧g(x)のとき、

　　

問　２つの曲線y=(x−1)³とy=x²−1によって囲まれた２つの部分の面積を求めよ。

【解】２曲線の概形は次のとおり。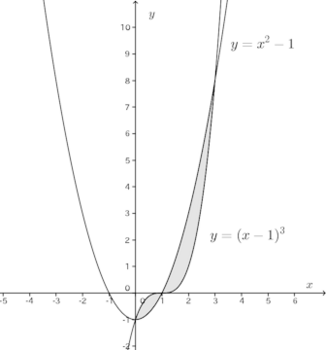



y=(x−1)³とy=x²−1との交点のx座標を求める。

　　

0≦x≦1では、y=(x−1)³≧y=x²−1
1≦x≦2では、y=x²−1≧y=(x−1)³
よって、求める面積Sは
　　

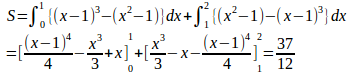
（解答終わり）

タグ：微分積分

数列の問題

数列の問題

問題　nを２より大きな自然数とする。

（１）　が成り立つことを用いて、

　　

であることを証明せよ。

（２）　さらに

　　

であることを証明せよ。

この問題は、実際に大学入試の問題として出題されたもの。

この問題の（１）はともかく、（２）はしびれてしまう。

入試問題としては適切だとは思わないが、この問題は非常に興味深い問題だと思う。

というわけで、解いてみることにする。

【解】

（１）　nが２より大きな自然数だから

　　

よって

　　

上の式の右辺は初項１、公比1/2の等比数列の１〜n項までの和だから

　　

したがって、

　　

（２）　nが２より大きい自然数だから

　　

よって、

　　

また、

　　

①に代入すると

　　

（解答終わり）

 

この問題を真似すると、

　　

したがって、

　　

よって、

　　

である。

　　

とすると、この数列（級数）はnの単調増加で、かつ、任意のnについて

　　

が成立し、有界で、この数列は収束する。この極限をSとおく、つまり、

　　

とおく。

ところで、マクローリン展開のところで

　　

をやった。

x=1を⑨に代入すると

　　

となり、

　　

である。
だから、

　　

という近似値は、結構、いい近似であることがわかる。

さらに、nが４以上のとき

　　

を利用すると、

　　

となり、Sと小数第４位まで一致する。

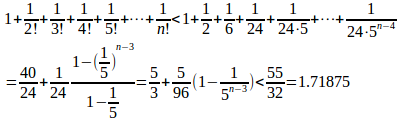
参考として、ねこ騙し数学の微分・積分の第１４回ネイピア数の記事をあげておく。

http://nekodamashi-math.blog.so-net.ne.jp/2015-03-05

タグ：数列 級数