微分積分 関数の増減と極大・極小 [ネコ騙し数学]
微分積分 関数の増減と極大・極小
区間Iに属す任意の2数をx₁、x₂とする。
単調増加関数と単調減少関数をあわせて単調関数いう。
平均値の定理を再掲する。
平均値の定理
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能であるならば
さらに、次の定理。
定理
関数f(x)が閉区間[a,b]で連続、開区間(a,b)で微分可能とする。開区間(a,b)でつねにf'(x)>0であれば、f(x)は開区間[a,b]で増加関数
開区間(a,b)でつねにf'(x)<0であれば、f(x)は開区間(a,b)で減少関数である。
【証明】開区間(a,b)でつねにf'(x)>0であれば、f(x)は開区間[a,b]で増加関数を証明する。
a≦x₁<x₂≦bとすれば、f(x)は[x₁,x₂]で連続、(x₁,x₂)で微分可能である。したがって、平均値の定理から
仮定よりf'(ξ)>0、x₂−x₁>0だから
開区間(a,b)でつねにf'(x)<0であれば、f(x)は開区間(a,b)で減少関数についても同様である。
(証明終わり)例
定義
x=aの近傍でf(a)がf(x)の最大値であるとき、関数f(x)はx=aにおいて極大であるといい、その値f(a)を極大値という。また、x=aの近傍でf(a)がf(x)の最小値であるとき、関数f(x)はx=aにおいて極小であるといい、その値f(a)を極小値という。
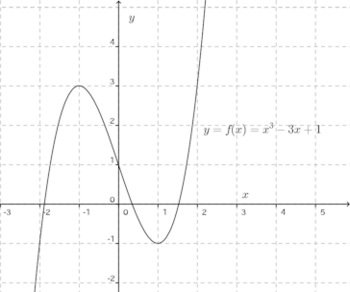
極大値、極小値をあわせて極値という。先に述べたf(x)=x³−3x+1の場合、x=−1の近傍、すなわち、δ>0が1に比べて十分小さいときx=−1の近傍、(−1−δ,−1+δ)でf(−1)=3が最大値なのでf(−1)=3はf(x)の極大値ということになる。同様に、x=1の近傍、(1−δ,1+δ)でf(1)=−1は最小値だからf(1)=−1はf(x)の極小値である。
また、この図から明らかなように、極大値は必ずしもf(x)の最大値にならないし、同様に極小値も必ずしもf(x)の最小値にならない。ちなみに、f(x)=x³−3x+1には最大値、最小値は存在しない。
定理(極値をとるための必要条件)
f(x)が区間Iで微分可能のとき、この区間のx₀でf(x)が極値をとるならば、f'(x₀)=0でなければならない。【証明】
f(x)がx=x₀で極大値をもつとき、x₁<x₀<x₂をみたす任意のx₁、x₂を区間内にとれば、f(x₁)<f(x₀)、f(x₀)>f(x₁)だから
極小のときも同様である。
(証明終わり)上の定理は、区間Iで微分可能な関数f(x)が極値をもつための必要条件であって、十分条件ではないこの注意する。
例 y=x³を微分するとy'=3x²。x=0でy'=0となるが、y=x³は単調増加関数で極値を持たない。
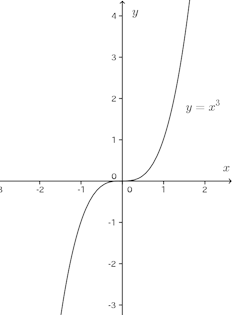
極値の判定法として次の定理をあげる。
定理
f'(a)=0かつx=aの前後でf'(x)が正から負に変われば、x=aで極大である。f'(a)=0かつx=aの前後でf'(x)が負から正に変わればx=aで極小である。
f'(a)=0かつx=aでf'(x)の符号が変わらなければ、f(a)は極値でない。上の定理を使うと、y=x³の場合、y=3x²で、x=0の前後のf'(x)の符号は+であり、符号が変わらないので、極値でないことが分かる。
問題1 次の問いに答えよ。
(1) 関数y=x³+3x²+12x−1はつねに増加関数であることを証明せよ。(2) 関数y=x³+ax²+12x−1が単調増加であるためのaの範囲を求めよ。
【解】(1)
(2) y'=3x²+2ax+12
これが単調増加であるためには、すべてのxについてy'≧0でなければならない。したがって、2次方程式3x²+2ax+12=0の判別式をDとすると、D≦0でなければならない。
問題2 次の関数の増減を調べ、グラフをかけ。
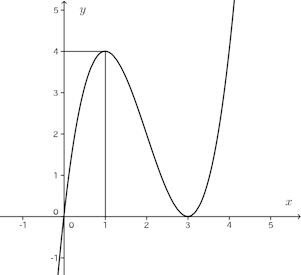
(1) y=x³−6x²+9x(2)
(1)
x | … | 1 | … | 3 | … |
y' | + | 0 | − | 0 | + |
y | 増加 | 4(極大) | 減少 | 0(極小) | 増加 |
(2)
y'=3x²+1>0