関数の増減と極値２

関数の増減と極値２

問題１　次の関数のグラフをかけ。

　　

【解】

　　

である。

よって、|x|≧1のとき

　　

この増減表を書くと

x	…	−1		1	…	2	…
f'(x)	+				−	0	+
f(x)	増加	−1		1		−1	増加

|x|<1のとき

　　

増減表を書くと

x	−1	…	0	…	1
f'(x)		−	0	+
f(x)	−1	減少	−3	増加	1

よって、グラフは次のようになる。

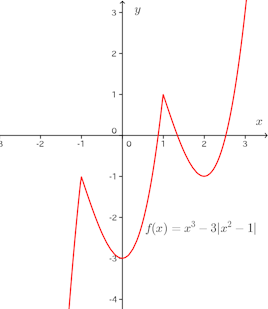
（解答終わり）

このグラフを見ると、f(x)がx=±1のところで局所的な最大である極大、x=0とx=2のところで局所的な最小である極小になっていることが分かると思う。

特にf(x)が極大になるx=±1のところに注目して欲しいのだけれど、ここは曲線が尖っていて微分可能ではない。つまり、f'(x)=0でなくても――そもそも微分係数が存在しない――、極値をとることがあるので注意が必要である。

ちなみに、

　　

である。

何故ならば、絶対値の中が非負、すなわち、x²−1≧0になるのは、x≦−1、x≧1のときであり、負になるのは−1<x<1のときだから。

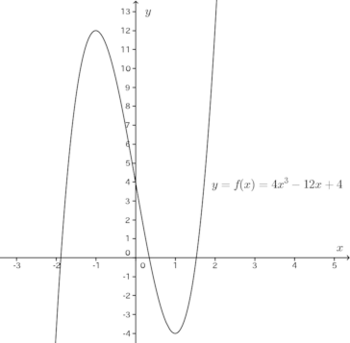
問題２　３次関数f(x)=4x³−3ax+bが極大値12と極小値−4をもつようにa、bの値を定めよ。

【解】

　　

極値をとるところではf'(x)=0でなければならないので、

　　

増減表を書くと

x	…		…		…
f'(x)	+	0	−	0	+
f(x)	増加	極大	減少	極小	増加

よって、

　　

これを解くと、a=4、b=4。

（解答終わり）

問題３　y=f(x)は３次関数で、そのグラフは原点に対して対称であり、x=1/2のときyは極小値−1をとる。y=f(x)を定め、yのグラフをかけ。

【解】

　　

とする。原点に対称なので

　　

よって、

　　

微分すると

　　

極値をとる点ではf'(x)=0でなければならないので

　　

また、

　　

これを解くと、a=4、c=−3。

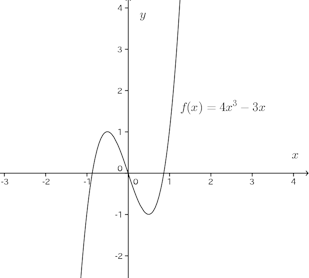
よって、f(x)=4x³−3x。

グラフは次の通り。

（解答終わり）

この関数は原点対称なので、計算するまでもなく、x=1/2で極小値−1をとることから、x=−1/2で極大値1である。

問題に原点に対して対称とあるので、この関数は奇関数であり、

　　

として議論をはじめてもいい。

問題４
（１）　y=x²(a−x)の極大値を求めよ。

（２）　その極大値は、定数aが変わると、どのように変わるか。これ図示せよ。

【解】

（１）　y'=2ax−3x²=x(2a−3x)

これを0とする値は

　　

a>0のとき、f(x)はx=0のとき極大で、極大値f(a)=0

a=0のとき、f(x)は単調減少で極大値はない。

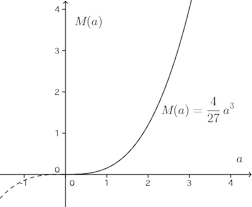
a>0のとき、f(x)はx=2a/3で極大で、

　　

（２）　極大値をM(a)とすると、グラフは次のようになる。

タグ：微分積分