微分の方程式への応用

微分の方程式への応用

問題１　次の方程式の実数解の個数はどのようになっているか。

（１）　x³−3x+1=0

（２）　x³−12x−a=0

【解】

（１）

　　

とおき、その増減を調べる。

　　

だから、増減表は次のとおり。

x	−∞	…	−1	…	1	…	+∞
f'(x)		+	0	−	0	+
f(x)	−∞	増加	3	減少	−1	増加	+∞

グラフは次のとおり。

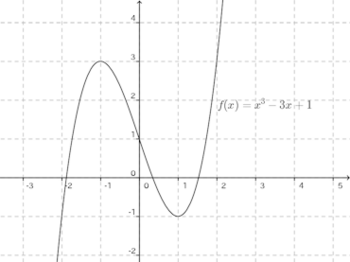
よって、実数解は３個。
x³−3x+1=0のα<β<γとする。

f(−2)=−1<0、f(−1)=3>0、f(1)=−1<0、f(2)=3>0だから、

中間値の定理より、α、β、γは−2<α<−1、−1<β<1、1<γ<2に存在する。

（２）

x³−12x−a=0は、連立方程式y=x³−12xとy=aと同値。

y=x³−12xの増減を調べる。

　　

よって、増減表は次のとおり。

x	−∞	…	−2	…	2	…	+∞
y'		+	0	−	0	+
y	−∞	増加	16	減少	−16	増加	+∞

y=x³−12xとy=aとの交点の数を調べる。

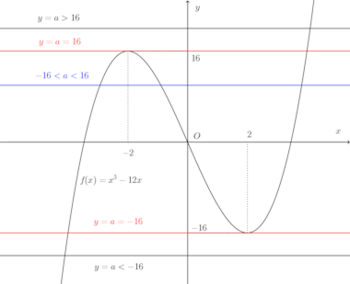
グラフより、

a>16のとき　１

a=16のとき　２

−16<a<16のとき　３

a=−16のとき　２

a<−16のとき　１

よって、実数解の個数は

a>16のとき　１

a=16のとき　２

−16<a<16のとき　３

a=−16のとき　２

a<−16のとき　１

である。
（解答終わり）

問題２　次の方程式が異なる３つの実数解をもつようにaの値を定めよ。

　　

【解】

　　

として、関数の増減を調べる。

　　

a≦0のとき、f(x)は単調増加で、

　　

なので、f(x)=0を満たす実数解は１個で不適。

よって、a>0でなければならない。

f(x)の増減表は

 

x	−∞	…	−√a	…	√a	…	+∞
f'(x)		+	0	−	0	+
f(x)	−∞	増加	2a√a+1	減少	−2a√a+1	増加	∞

f(x)=0が実数解を３個もつためには、

　　

でなければならないので、

　　

よって、

　　

【解答終わり】

問題４

　　

とする。

（１）　y=f(x)の増減を調べて、方程式f(x)=0は１つの実根をもつことを証明せよ。

（２）　方程式g(x)=0は実根を持たないことを証明せよ。

【解】

（１）

　　

よって、f(x)は単調増加。

f(−2)<0、f(−1)>0だから、f(x)=0の解は−2<x<−1にただ１つ存在する。

（２）

　　

f(x)=0の実根をαとすると、x<αでf(x)<0、x>αでf(x)>0。

よって、g(x)は、x=αで極小値（最小値）をとる。

　　

よって、g(x)は実根を持たない。

（解答終わり）

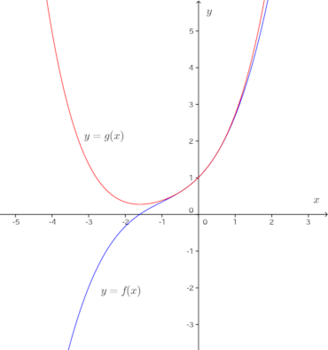
このグラフを見ると、−1≦x≦1で、f(x)とg(x)の値がよく一致していることが分かる。

　　

だから、（誤）差はx=±1のところで最大で、最大誤差は1/24。

ところで、マクローリン展開のところで

　　

という公式が出てきた。

だから、この問題に出てくるf(x)やg(x)は、指数関数のべき乗展開の近似式と考えることができる。

このグラフに指数関数の曲線を加えると、次のようになる。

 

タグ：微分積分