微分の不等式への応用

微分の不等式への応用

問題１　次の不等式を証明せよ。

（１）　x>1のとき

　　

（２）　a>0、x≧0のとき

【解】

（１）　左辺と右辺の差をとり

　　

とする。

f(x)はx>1で微分可能。

　　

よって、f(x)はx≧1で単調増加。

したがって、x>1で

　　

すなわち、

　　

である。

（２）　左辺と右辺の差をとり

　　

とする。

f(x)はx>0で微分可能。

　　

よって、f(x)は0≦x<aで減少、a<xで増加し、f(a)は極小値（最小値）である。

したがって、

　　

（証明終わり）

問題２ a、b、cが正の数であるとき、

　　

の値の増減を調べることにより、次の不等式を証明せよ。

　　

【解】

　　

よって、f(x)はx=√abのときに極小（最小）。

　　

つまり、

　　

x=cとすれば、

　　

（解答終わり）

a³=α、b³=β、c³=γ（α>0、β>0、γ>0）とすると、上の式は次のように書き換えることができる。

　　

この公式を使うと、

　　

の最小値を微分を使わずとも、次のように求めることができる。

　　

等号成立は

　　

のときだから、これを満たすxは存在する。

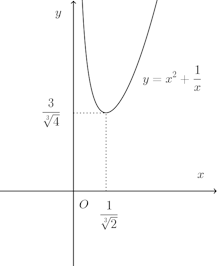
相加平均≧相乗平均を使って最小値を求めるとき、等号を満たすxが存在することを確かめないといけない。

等号が成立するxが存在しない場合もあるのでこの確認は絶対しなければならない。

この程度ならば、微分したほうが楽。

　　

だから、のときに極小値をもつことが分かる。

上の問題では、f(x)の定義域をx>0としているけれど、

　　

とすれば、f(x)は次のようになる。

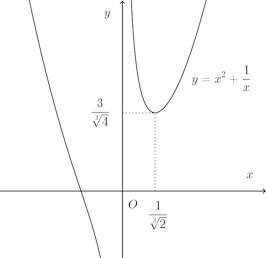
この図から明らかなように、極小値は存在するけれど、最小値は存在しない。

また、y=aとy=f(x)との交点を調べることにより、３次方程式

　　

の実数解の個数を調べることができる。

何故ならば、

　　

だから。

この結果を使うと、

a>□のとき実数解は３つ、a=□のとき実数解は２つ、a<□のとき実数解は１つと判別することができる。

ちなみに、1/xの微分は導関数のところで求めてある。