定積分と面積の問題２

定積分と面積の問題２

問題１　放物線y=x²上の任意の２点P、Qにおける接線の交点をRとするとき、P、Qの位置に関係なく、放物線は△PQRの面積を2:1に分けることを示せ。

【解】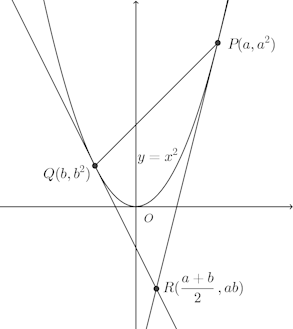

P(a,a²)、Q(b,b²)とすると、P、Qにおける接線の方程式は

　　

よって、交点Rは

　　

直線PQの方程式は

　　

△PQRの面積Sは

　　

直線PQと放物線y=x²で囲まれた図形の面積S₁は

　　

放物線y=x²と２つの接線とで囲まれた図形の面積をS₂とすると

　　

よって、S₁:S₂=1:2で、放物線は△PQRの面積を2:1に分ける。

（解答終わり）

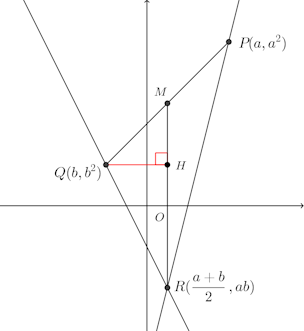
△PARの面積は、PQの中点をMとすると

　　

になるので、線分RMの長さは

　　

△MQRの高さQHは

　　

で、

　　

同様に、

　　

したがって、

　　

と、積分をすることなく簡単に求めることができる。

積分でこの面積を求めるのならば、

　　

を計算すればよい。

また、
　　

の計算では、

　　

という公式（？）を用いている。

問題２　直線y=xと放物線y=x²−xとが囲む面積がy=ax（a>0）で２等分されるようにaの値を定めよ。

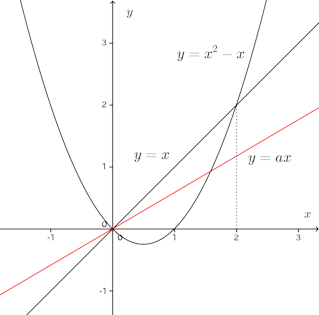
【解】

直線y=xと放物線y=x²−xとが囲む面積Sは

　　

y=axと放物線y=x²−xの交点のx座標を求めると、

　　

だから、y=axと放物線y=x²−xが囲む面積S₁
　　

条件より2S₁=Sだから

　　

（解答終わり）

 

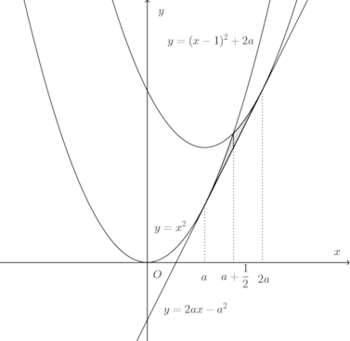
問題３　２つの放物線y=x²、y=(x−1)²+2aがある。

（１）　これらの共通接線の方程式とその接点の座標を求めよ。

（２）　これら２つの放物線と共通接線とで囲まれる部分の面積を求めよ。

【解】

（１）　y=x²上の点(α,α²)における接線の方程式は

　　

これが放物線y=(x−1)²+2aと接する。

よって、次の２次方程式

　　

は重根をもつ。この２次方程式の判別式をDとすると

　　

a=αのとき

　　

よって、共通接線は

　　

接点は、(a,a²)、(a+1,a²+2a)である。

（２）　放物線y=x²、y=(x−1)²+2aの交点のx座標を求めると、x=a+1/2だから、求める面積は

　　　　

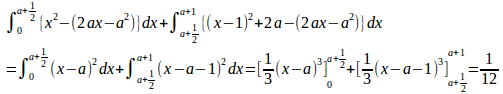
（解答終わり）

問題４　0≦a≦2のとき、y=x²(x−2)とy=ax(x−2)とで囲まれる部分の面積の最大値と最小値を求めよ。

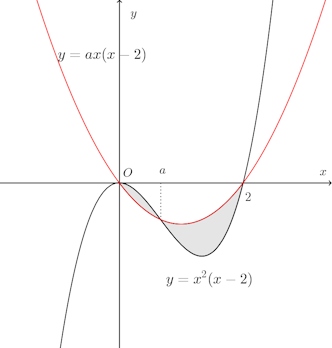
【解】

２つの曲線の交点のx座標は

 　　

よって、x=0,a,2である。

面積S(a)とすると

　　

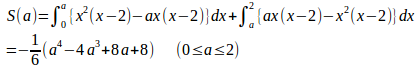
よって

　　

0≦a≦2では、

　　

だから、S(a)の増減表は

a	0	…	1	…	2
S'(a)		−	0	+
S(a)	4/3	減少	1/2	増加	4/3

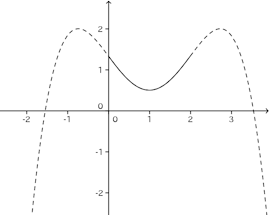
よって、

a=1/2のとき最小で最小値は1/2

a=0、2のとき最大で最大値は4/3

（解答終わり）

タグ：微分積分