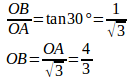何でも、微分積分を使えばいいというものではない [ネコ騙し数学]
何でも、微分積分を使えばいいというものではない
問題
図中には、直線ABと4分円C、x軸、y軸とで囲まれた領域を斜線で示してある。
(1) 斜線部の面積を求めよ。(2) 斜線部をx軸のまわりに回転させてできる立体の体積を求めよ。
ねこ騙し数学では、現在、微分積分の問題演習をやっているので、おそらく、多くの人はこの問題を微分積分を使ってとこうとするに違いない。
しかし、それは、まさしく、「牛刀をもって鶏を割く」である。この問題は、微分積分を使わず中学3年生程度の数学の知識だけで簡単に解けてしまう問題であって、そもそも、微分積分を使う必要がないのだ。
積分を使って解こうとすると、
したがって、求めるべき面積は
もっとも、この積分は半径2の4分円の面積になるので、π×2²÷4=πになることがすぐにわかる。
このような図形的な解答をするのであるならば、
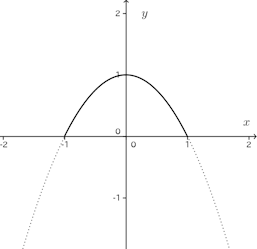
①より、Bのy座標は4/√3だから、
こうすれば、
先に述べたように、積分の計算は一切、不要である。
いやいや、最初から、次のように解くべきだ。
求めるべき面積は、△OABの面積から半径2の4分円の面積を引いたもの。
点Pの座標は(1,√3)だから、接線ABの方程式は
したがって、
点Pの座標は
円:x²+y²=r²の円周上の点(x₀,y₀)における接線の方程式は
実は、この問題、接線の方程式すら求める必要がない。
∠OAP=30°だから、
(2)は、積分を使うと、
しかし、この問題も図形的な考察から、次のように簡単に解けてしまいます。
求めるべき体積は、△ABOをx軸のまわりに回転してできる円すいの体積から半径2の4分円をx軸のまわりにできる半球の体積を引いたもの。したがって、
体積 [ネコ騙し数学]
体積
§1 一般の立体の体積
立体をx軸に垂直な平面で切ったときの断面積がxの関数S(x)であるとき、この立体のx=aとx=bとの間の体積Vは
例 底面積A、高さhの角すいの体積
角すいの頂点を原点Oに、Oから底面におろした垂線をx軸にとる。すると、x軸に垂直な平面が角すいを切り取る断面積S(x)は
問題1 底面の半径がaであるような直円柱がある。底面の直径を通り、底面と45°の角をなす平面でこの直円直円柱を切り、この平面と底面および側面で囲まれた立体を作る。この立体の体積を求めよ。
【解】底面の中心をOとし、底面の直径をx軸にとる。
x座標がxである点をとおりx軸に垂直な平面によって切り取られる立体の断面は、直角2等辺三角形で、その断面積S(x)は
§2 回転体の体積
(1) 曲線y=f(x)(a≦x≦b)とx軸とで囲まれた部分をx軸のまわりで回転してできる立体の体積
(2) 曲線x=g(y)(c≦y≦d)とy軸とで囲まれた部分をy軸のまわりで回転してっできる立体の体積は
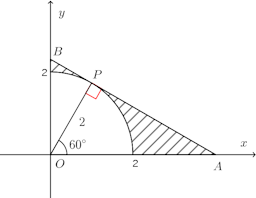
問題2 曲線y=1−x²とx軸で囲まれた図形が、x軸のまわりを回転してできる立体の体積をV₁、y軸のまわりを回転してできる立体の体積をV₂を求めよ。
【解】回転させる図形は次の通り。
したがって、x軸のまわりで回転させて得られる図形の体積V₁は
y軸のまわりで回転させて得られる図形の体積V₂は
(3) 2つの曲線y=f(x)、y=g(x)(f(x)≧g(x)≧0,
a≦x≦b)で囲まれた部分をx軸のまわりに回転してできる回転体の体積Vは
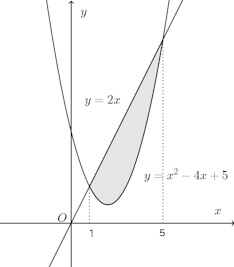
問題3 放物線y=x²−4x+5と直線y=2xとで囲まれた図形をx軸のまわりに回転してできる立体の体積を求めよ。
【解】y=x²−4x+5とy=2xの交点のx座標は、x=1、x=5。