(a+b)²−(a−b)²をどうやって計算する? [ネコ騙し数学]
一つ質問するけれど、
真面目に展開して、
それとも、
この場合は、①の方が楽だけれど、今日のワンポイントゼミ3にでてきた
あなたは、これを真面目に展開して計算しますか。
オレは、頭の中で、②を使って、
①の結果、
⑧をバカ正直に展開して計算するヒトは、⑨未満と呼ばれてもしょうがない!!
そう、思わないかい?
⑨のチルノですら、間違っているけれど、自身の知識を活用している!!
ワンポイントゼミ3 球の体積 [ネコ騙し数学]
ワンポイントゼミ3 球の体積
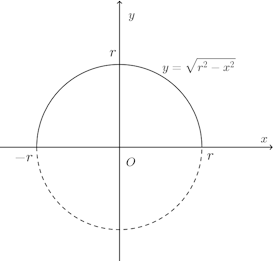
半径rの円の体積Vは
このことを定積分を使って求めることにする。
原点Oを中心とする半径rの半円は
は偶関数だから、偶関数の定積分の性質から
途中計算でこれを使っている。
【方法2】
原点を中心とする球の方程式は
この断面の面積S(t)は
方法2の定積分は、方法1の計算のxがtに変わっているだけなので、計算しないけれど、このように計算することもできる。
(※) x=±rにおける球の断面(?)を半径0の円とみなしている。
厳密には
問題 半径rの円
【解】
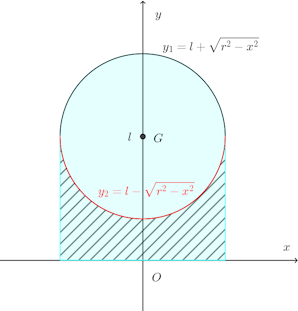
求める体積は、薄い水色で示されている、y₁とx軸とで囲まれている領域を回転してできる立体の体積から、斜線部で示されているy₁とx軸とで囲まれている領域を回転してできる立体の体積を引いたもの。
したがって、
注目して欲しいのは、この結果。
⑨より、問題で求めた円環体の体積Vは
円環体の体積V=(円Cの重心が回転により描く軌跡の長さ)×(円Cの面積)
になっていることがわかる。
これは偶然のことか(^^)
体積の問題2 [ネコ騙し数学]
体積の問題2
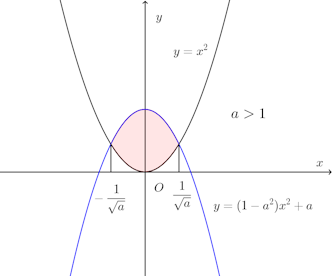
問題1 異なる2つの放物線y=x²、y=(1−a²)x²+aが交わるとき、これらで囲まれる図形をy軸のまわりに回転してできる回転体の体積は、aの値にかかわらず一定であることを証明せよ。ただし、a>0とする。
【解】異なる2つの放物線の交点のx座標は
(1) 0<a<1のとき、体積Vは
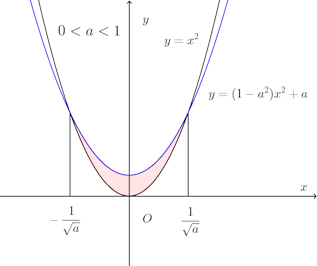
(2) a>1のとき
よって、体積Vはaの値にかかわらず一定で、その値はπ/2である。
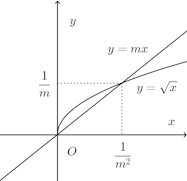
(解答終わり)問題2 曲線y=√xと直線y=mxとで囲まれる図形をx軸のまわりに回転してできる立体とy軸のまわりに回転できる立体
とが同じ体積になるようにmの値を定めよ。
だから
問題2 図のように、AC=1、BC=3とし、DEはA、Bを中心とし点Cで外接する2円の共通接線である。∠ABE=60°であることを示し、斜線をつけた部分CDEをABのまわりに回転して得られる立体の体積を求めよ。
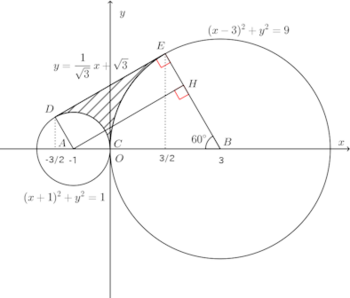
【解】
Cを原点Oにとり、Aを(−1,0)、Bを(3,0)にとる。
Aから直径BEに垂線をおろし、垂線の足をHとする。
四角形ADEHは長方形。
よって、
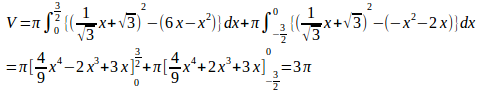
(解答終わり)