ワンポイントゼミ４ 微分を用いて、整式を(x−a)²で割った余りを求める

ワンポイントゼミ４　微分を用いて、整式を(x−a)²で割った余りを求める

問題　f(x)を２次以上の整式とする。

（１）　f(x)を(x−a)²で割ったときの余りが

　　

であることを証明せよ。

（２）　f(x)がf(x)を(x−a)²で割り切れるための必要十分条件がf(a)=f'(a)=0であることを証明せよ。

（３）　x⁷−2x+4を(x−1)²で割った余りを求めよ。

【解】

（１）　f(x)をf(x)を(x−a)²で割った商をQ(x)、余りをpx+qとすると

　　

xで微分すると、

　　

①、②にx=aを代入すると、

　　

④よりp=f'(a)、これを③に代入すると、

　　

よって、余りは

　　

である。

（２）

【⇒の証明】

（１）より、f(x)を(x−a)²で割ったときの余りは

　　

仮定より、f(x)を(x−a)²で割り切れるので、f(x)を(x−a)²で割ったときの余りは０である。

したがって、

　　

でなければならない。

これが任意のxについて成り立つので、

　　

⑤より、f'(a)=0。

⑥より

　　

したがって、f(a)=0、f'(a)=0である。

【逆の証明】

f(x)を(x−a)²で割ったときの余りは

　　

仮定より、f(a)=0、f'(a)=0。

したがって、

　　

以上のことより、

f(x)がf(x)を(x−a)²で割り切れるための必要十分条件がf(a)=f'(a)=0である。

（３）

　　

よって、

　　

（１）より、余りは

　　

（解答終わり）

 

　　

をxで微分するとき、次の微分公式を使っている。

　　

この公式を使うと、

　　

(x−a)²の微分で、もう一度、微分公式を用いると、

　　

したがって、

　　

となる。

もちろん、

　　

と計算してもよい。

また、同様の議論から、

　　

　　――n=2のとき、こうなることを確かめよ――

したがって、F(x)が整式であるとき、y=F(ax+b)をxで微分すると

　　

話を元に戻すが、

問題より、f(x)が整式であるとき、f(x)=0が重複解（重根）を持つための必要十分な条件は

　　

が共通解を持つことである。

タグ：微分積分

剰余の定理と因数定理、そして、解と係数の関係

剰余の定理と因数定理、そして、解と係数の関係

§１　剰余の定理

剰余の定理

整式f(x)をx−aで割った余り（剰余）はf(a)である。

【証明】

多項式f(x)をx−aで割った商をQ(x)、余りをRとすると、

　　

したがって、

　　

（証明終わり）

問　x²−3x+4をx−1、x−2で割った余りを求めよ。

【解】

f(x)=x²−3x+4とおく。

剰余の定理より、

f(x)をx−1で割った余りR₁は

　　

x−2で割った余りR₂は

　　

（解答終わり）

 

問題１　xについてある整式をx−2で割ると5余り、x−3で割ると8余るという。この整式を(x−2)(x−3)で割った余りを求めよ。

【解】

xについての整式をf(x)、(x−2)(x−3)で割った商をg(x)、余りをax+bとする（※）。

題意より

　　

x−2で割った余りが5だから、①より

　　

x−3で割った余りが8だから、①より

　　

②、③を解いてa=3、b=−1。

よって、余りは3x−1である。

（解答終わり）
（※）　整式f(x)を２次式(x−2)(x−3)で割った余りは、高々１次式なので、その余りをax+bと置くことができる。

§２　因数定理

因数定理

整式f(x)がx−aを因数にもつ必要十分な条件はf(a)=0である。

【証明】

f(x)をx−aで割った商をQ(x)、余りをRとする。

（必要条件の証明）

　　

f(x)はx−aを因数にもつので、R=0。

したがって、

　　

（十分条件の証明）

　　

上式にx=aを代入すると、

　　

仮定よりf(a)=0だから、R=0。

よって、f(x)はx−aで割り切れ、f(x)はx−aを因数にもつ。

（証明終わり）

問　次の方程式を解け。

　　

【解】

f(x)=x³−3x²−4x+12とおくと、

　　

よって、x³−3x²−4x+12はx−2を因数にもつ。

x−2でf(x)を割ると、商はx²−x−6。

だから、
　　

よって、この方程式の解はx=±2、3である。

（解答終わり）

§３　２次方程式と３次方程式の解と係数の関係。

（１）　２次方程式の解と係数の関係

２次方程式の一般形は

　　

この解をα、βとすると、因数定理より

　　

となる。

したがって、

　　

となり、この恒等式が成立する条件から
　　

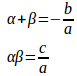
これを２次方程式の解と係数の関係という。

問題　２次方程式x²−10x+c=0の２つの実根αとβの間にβ=α³の関係が成立するとき、cの値を求めよ。

【解】

解と係数の関係より

　　

問題の条件よりβ=α³だから、
　　

f(α)=α³+α−10とするとf(2)=0。

よって、

　　

したがって、α=2。

　　

（解答終わり）

（２）　３次方程式の解と係数の関係

３次方程式の一般形は

　　

この解をα、β、γとすると

　　

よって、この恒等式の右辺と左辺を比較すると
　　

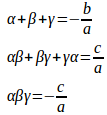
という３次方程式の解と係数の関係が得られる。

問題　方程式x³+ax²+bx−12=0が根3および3と異なる実根をもつとき、重根およびa、bの値を求めよ。

【解】

3と異なる実根をαとすると、解と係数の関係より

　　

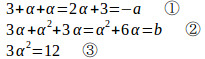
③より

　　

①、②より

　　

だから、

α=2のとき、a=−7、b=16

α=−2のとき、a=1、b=−8

（解答終わり）