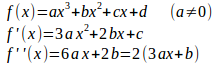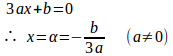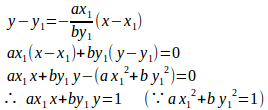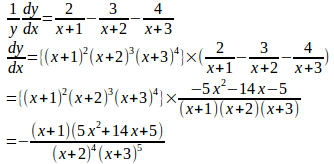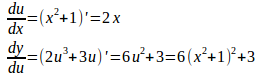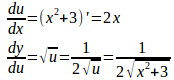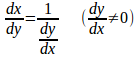3次関数と変曲点 [ネコ騙し数学]
3次関数と変曲点
問題1 f(x)=x³+3x²−4x−6とするとき、関数y=f(x−a)+bのグラフの変曲点が原点に一致するようにa、bの値を定めよ。
【解】
(−1,0)を原点(0,0)と一致させるためには、x軸の正の方向に1だけ移動させれば良いので、a=1、b=0である。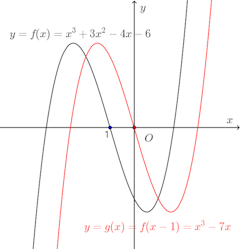
f(x)=x³+3x²−4x−6をx軸の正方向に1平行移動させた関数をg(x)とすると、
そして、g(x)は
y=f(x)の変曲点が原点になるように変換、平行移動したのだから、これは当たり前。
そして、このことから、y=f(x)がその変曲点(−1,0)に関して対称であることが分かる。さて、このことが一般の3次関数y=f(x)=ax³+bx²+cx+d(a≠0)について言えるのか、つまり、3次関数は変曲点に関して対称なのか、このことを確かめたい。
問題2 3次関数y=f(x)のグラフはただ1つの変曲点をもち、その変曲点に関して対称であることを証明せよ。
【解】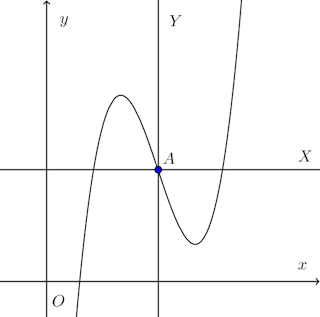
f''(x)=0を解くと
であり、x=αの前後でf''(x)の符号が変化するからA(α,f(α))は変曲点である。
そして、この点以外でf''(x)の符号が変わることはないから、3次関数の変曲点はAただ一つである。
Aが原点に来るように座標軸を平行移動すると、新座標軸XAYに関して曲線の方程式は
したがって、y=f(x)は変曲点Aに関して対称である。
(証明終わり)3次関数のグラフは変曲点に関して対称であることが証明された。
問題3 3次関数f(x)=x³+3ax²+3bx+cがx=αのとき極大、x=βのとき極小になるとき、
(1) f(α)+f(β)をa、b、cであらわせ。(2) y=f(x)の極大になる点、極小になる点をそれぞれA、Bとすれば、線分ABの中点Mはこの曲線上にあることを証明せよ。
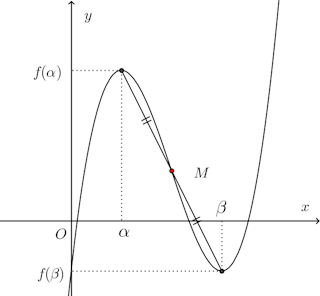
【解】
(1)
(2) A、Bの中点をM(p,q)とすると、
(解答終了)
この関数の変曲点を求めると、
つまり、変曲点は、上で求めた極大点Aと極小点Bの中点である。
逆関数の微分の問題 [ネコ騙し数学]
逆関数の微分の問題
問題1 次の関係式よりをxの式で表せ。
(1) x=sinyの両辺をyで微分すると
(2) x=cosyの両辺をyで微分すると
−π/2<y<π/2で定義されたx=sinyという関数の逆関数を
高校の数学の範囲を超えるけれど、
である。
問題2 x=tany(−π/2<x<π/2)を利用して、tanyの逆関数の微分を求めよ。
【解】x=tanyの両辺をyで微分すると
したがって、
問題3 図のようなグラフで表される関数をy=f(x)(0≦x≦a)とし、この式をxについて解いて得られた式をx=g(y)とする。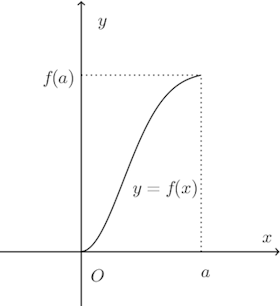
(2) 次の値を求めよ。
(1) y=f(x)と同じグラフ。
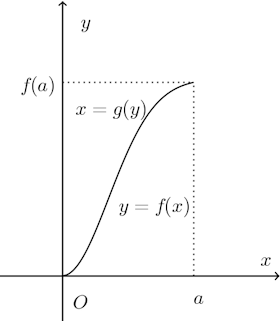
(2) 図のように、y=f(x)とx軸、x=aで囲まれた図形の面積をS₁、x=g(y)とy軸、y=f(a)で囲まれた図形の面積をS₂とする。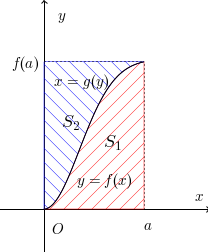
この問題の(1)で、「何故、同じグラフになるか」という質問は、「1=1が何故、成立するか」という質問と同じ。
「逆関数の定義からこうなる」と答えるしかない!!そして、このような質問をするヒトは、逆関数を理解していない!!
y²=f(x)のグラフの概形をかく [ネコ騙し数学]
y²=f(x)のグラフの概形をかく
陰関数の定義
x、yの関係式f(x,y)=0に対して、関数y=φ(x)が
を満たすとき、y=φ(x)をf(x,y)=0によって定まる陰関数という。
とって付けたように、陰関数の定義をあらたに与えたところで、さっそく、問題。
問題1 方程式y²=x⁴−2x²によって表される曲線のグラフをかけ。
【解】
また、
yは実数だからy²≧0。よって、
この関数は偶関数だから、x≧0について考えればよい。(x<0のグラフの部分はx>0のグラフをx軸で折り返せばよい)
つまり、
これを微分すると(※)
x | 0 |
| √2 | … | √3 | … |
y'' |
|
|
| − | 0 | + |
y |
|
|
| 上に凸 | 変曲点 | 下に凸 |
まず、このグラフをかき、それをy軸で折り返す。
で、
以上のことより、次の図になる。
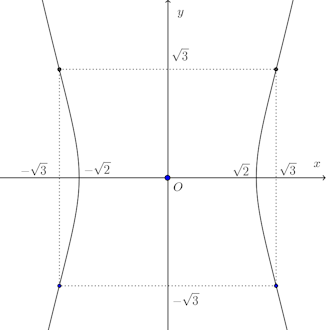
(解答終わり)
なのですが、この曲線は問題1の解答の
この組み合わせで考えると、いくらか楽になる。
なお、この曲線(?)上の点は(0,0)にも存在する。この点(0,0)のように、その近傍にそれ以外に曲線上の点が存在しない点のことを孤立点という。
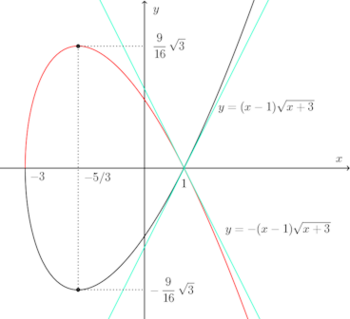
問題2 関数の増減を調べて次の方程式のあらわす曲線の概形をかけ。
(1) y²≧0だから、x≧−3。
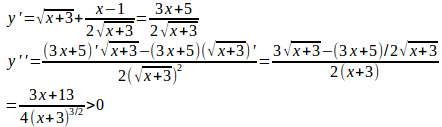
したがって、yは、x=−5/3で極小値をとり、極小値は−16√3/9。
(2)
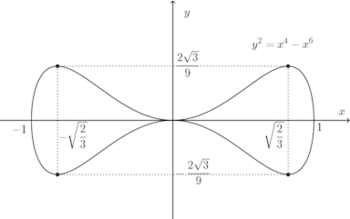
(解答終わり)
高校の微分積分の範囲内でも、これらの曲線の概形を描くことはできるけれど、これらは大学の数学の範囲でしょう。
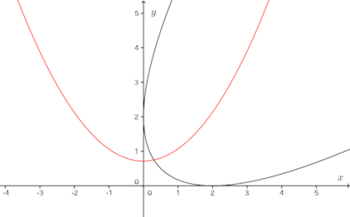
問題3 定点(1,1)を通り、定直線x+y=0に接する円の中心P(x,y)の軌跡をCとするとき、軌跡Cの方程式を求め、そのグラフをかけ。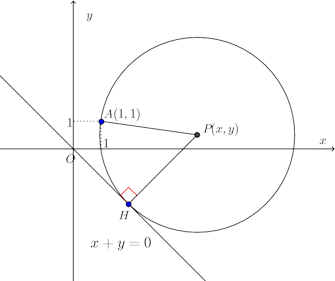
定点(1,1)をA、P(x,y)から直線x+y=0に下ろした垂線の足をHとすると、PA=PH=円の半径である。よって、
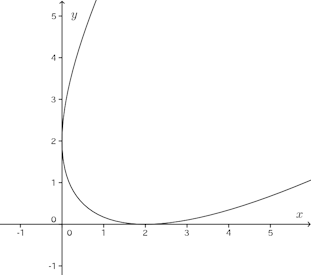
(解答終了)
この曲線の正体が何か、少しわかりづらいと思うのですが、この曲線を45°反時計回りに回転させると、次のような曲線になり、この曲線の正体が放物線であることがわかる。
陰関数の微分の問題 [ネコ騙し数学]
陰関数の微分の問題
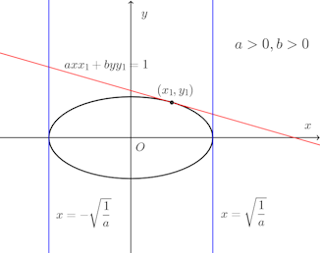
問題1 陰関数の微分法を用いて、次の方程式によって表された曲線上の点(x₁,y₁)における接線の方程式を求めよ。ただしa≠0、b≠0とする。
【解】
(1) ax²+by²=1の両辺をxで微分すると、
y₁=0のとき、a>0のとき、接線の方程式は
この場合も、
(3) xy=aの両辺をxで微分すると、
(解答終わり)
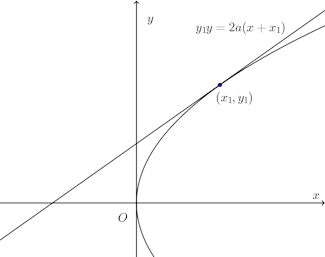
問題2 曲線
(解答終わり)
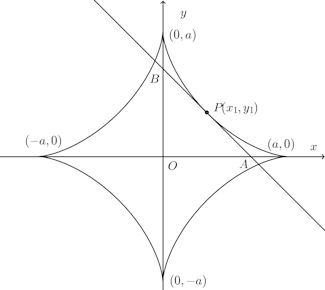
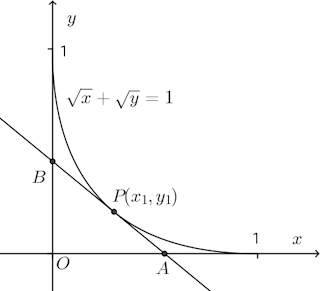
問題3 曲線
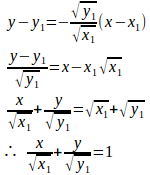
よって、x切片は√x₁、y切片は√y₁となり、
(解答終了)
補足

微分法を用いた不等式の証明 [ネコ騙し数学]
微分法を用いた不等式の証明
微分法を用いた不等式の証明は、例えば、f(x)>g(x)という不等式の場合、F(x)=f(x)−g(x)とし、微分法を用いてF(x)の増減を調べることが基本。
例 x²>2x−2を証明せよ。

このような問題があった場合、左辺と右辺の差をf(x)と置き、両辺をxで微分する。
したがって、
もっとも、この問題の場合、微分を使うまでもなく、
では、問題。
問題 x>0のとき、次の不等式が成り立つことを証明せよ。

【解】
(1)
とおく。
よって、

したがって、g'(x)はx>0で単調増加。
ゆえに、x>0で

(2)

とおく。
また、
①と②より、

(解答終わり)
(1)、(2)ともに、マクローリン展開(テーラー展開)を
有限項で撃ち切ったもの。
そして、(2)の

また、(1)の
という不等式が得られる。

図から明らかように、各辺のすべての関数が偶関数なのだから、さらに次の不等式が得られる。
なお、この不等式を得るにあたって、定積分の次の定理を使っている。
定理 f(x)、g(x)が[a,b]で連続、かつ、f(x)≧g(x)であるならば、
f=gは、fとgが同一の関数、つまり、x∈[a,b]のすべてのxに対してf(x)=g(x)である、ことをあらわしている。
宿題 x>0で
対数微分法 [ネコ騙し数学]
対数微分法
非零の値をとる微分可能なxの関数u、vがある。
その積をy=uvとおき、この絶対値
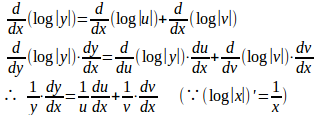
両辺にyをかけると
また、y=u/vとおき、この両辺の対数をとり、さらにそれを微分すると
このように、関数の対数をとって、さらに、微分する方法を対数微分法という。
問題1 次の関数を微分せよ。
両辺の対数をとり、微分すると
問題2 次の関数を微分せよ。
両辺の対数をとり、微分すると、
問題3 次の関数を微分せよ。
両辺の絶対値をとり、さらにその対数をとる。
以上のことから、
絶対値をとるのは、対数の真数となるyが負になることがあるから。対数の真数は正の数でないとならない。
なお、
x>0ならば
そこで、u=−1とおき、合成関数の微分を使う。
そして、このことから、
問題4 次の微分をせよ。
(解答)
問題4のように微分する関数が複雑な積の形で与えられているときに対数微分法は有効な計算方法。
陰関数の微分と媒介変数で表された関数の微分 [ネコ騙し数学]
陰関数の微分と媒介変数で表された関数の微分
§1 陰関数の微分
φ(x,y)=x²+y²−1=0のように2変数xとyの関係が与えられているとする。これをyについて解くと、
このように、φ(x,y)=0の形で与えられる関数を陰関数、y=f(x)の形で与えられる関数を陽関数という。
問1 x²+y²=1のとき、dy/dxを求めよ。
【解】x²+y²=1の両辺をxで微分すると
なお、dy²/dxの計算は、合成関数の微分の公式を用いて
問2 次の方程式からdy/dxを求めよ。a0、b、pは定数とする。
(1) 両辺をxで微分すると、
(2) 両辺をxで微分すると
(3) 両辺を微分すると
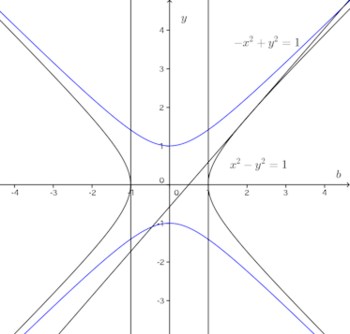
問題1 曲線x²−y²=9およびxy=4の交点における接線は互いに直交していることを証明せよ。
【解】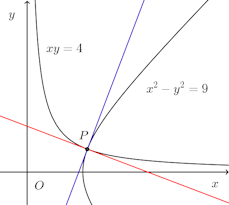
x²−y²=9の両辺をxで微分すると、
(解答終わり)
§2 媒介変数で表された関数の微分
x、yが変数tによってx=f(t)、y=g(t)で与えられているとする。
x=f(t)の逆関数が存在するとき、yはxの関数とみなすことができる。y=g(t)をの両辺をxで微分すると、
定理 (媒介変数tで表された関数の微分)
x、yがそれぞれtの関数であるとき、dy/dx≠0ならば
問 次の関係式より、dy/dxを求めよ。
(1)
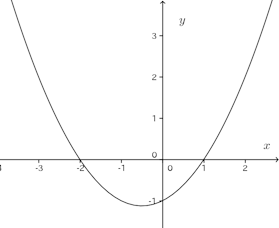
(2)
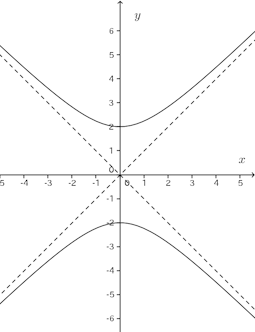
(解答終わり)
合成関数と逆関数のの微分 [ネコ騙し数学]
合成関数と逆関数のの微分
§1 合成関数の微分
写像の定義
合成写像の定義
X、Y、Zを集合、
このとき、x∈Xに対してg(f(x))∈Zを対応させる写像を合成写像(合成関数)といい、であらわす。すなわち、
たとえば、
合成関数の微分
先にでたように、
次に、より一般の合成関数y=f(g(x))の微分公式を求めることにする。
y=f(u)、u=g(x)がともに微分可能であるとする。
したがって、
定理 (合成関数の微分)
y=f(u)、u=g(x)がともに微分可能であるとき、合成関数y=f(g(x))の微分は
あたかも分数の約分のようであるから①は覚えやすい。
しかし、使い勝手がいいのは⑨である。問 次の関数を微分せよ。
(1) u=x²+1とおくとy=2u³+3u。
よって
(2) u=x³+3とおくとy=√u。
よって、
(2)の3をa²(aは定数)を置き換えると
§2 逆関数の微分
y=f(x)の逆関数をy=g(x)とおけば、x=f(y)
この両辺をxで微分すると、右辺は
よって
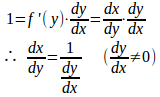
定理 (逆関数の微分公式)
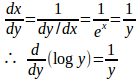
このxをyに置き換えると、
三角関数の接線の問題 [ネコ騙し数学]
三角関数の接線の問題
三角関数の微分公式
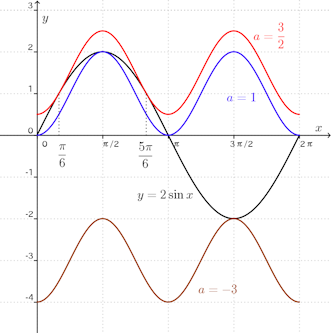
問題1 0≦x<2πの区間において、y=a−cos2xがy=2sinxのグラフと接するように、定数aの値を定めよ。
【解】2曲線y=a−cos2xとy=2sinxの接点Pの座標を(x₁,y₁)とすると、この2曲線が接するのだから
y=a−cos2xとy=2sinxの導関数を求めると
よって、x₁=π/6、π/2、3π/2、5π/6。
①より
x₁=π/2のとき、a=1。
x₁=3π/2のとき、a=−3。x₁=5π/6のとき、a=3/2。
よって、aの値は3/2、1、−3である。曲線y=f(x)とy=g(x)がx=aで接する条件は、
問題2 曲線y=sinx(0≦x≦2π)の接線がx軸およびy軸と交わる点をA、Bとし、原点をOとするとき、線分OA、線分OBの長さの比が√2:1になる場合の接点の座標を求めよ。
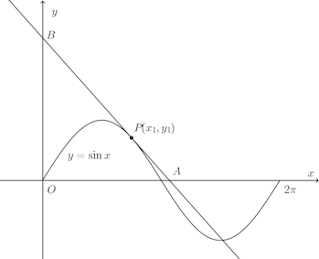
【解答】
接点Pを(x₁,sinx₁)とすると、y'=cosxだから、接線の方程式は
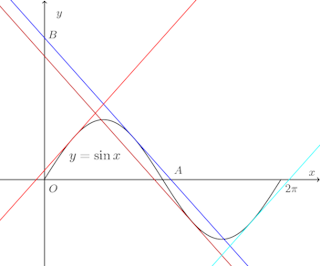
(解答終わり)
(※) OB/OAは直線の傾きの絶対値に等しい。
A(a,0)、B(0,b)とすると、OA=|a|、OB=|b|。そして、この2点を通る直線の傾きmは
問題3 関数y=tanxのグラフと、原点におけるそれの接線と交点の任意のひとつのx座標をaとする。このとき、関数y=sinxのグラフ上のx=aでこれに接する接線は原点を通ることを証明せよ。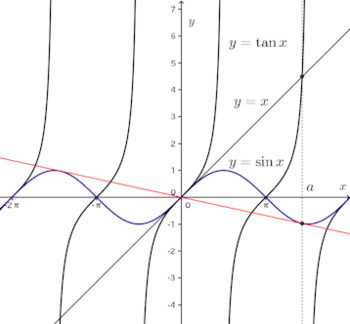
y=tanxとy=xの交点の一つのx座標をaとすると、
(解答終わり)
三角関数の微分 [ネコ騙し数学]
三角関数の微分
三角関数の導関数を求める前に、三角関数の公式を紹介。
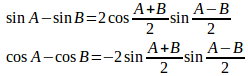
さらに、前回、求めた三角関数の極限の公式。
正弦関数f(x)=sinxの導関数を求めることにする。
余弦関数cosxの導関数も同様に
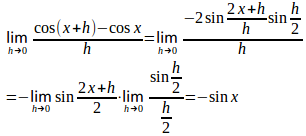
と求めることができる。
正接関数tanxの導関数も微分の定義から導くことができるけれど、少し複雑になるので、商の微分公式、
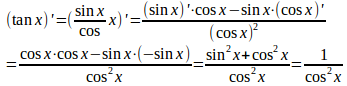
になる。
以上の結果をまとめると、三角関数の導関数は次のとおりである。
三角関数の微分の本格的な問題を解こうとすると、合成関数の微分法をはじめに三角関数の諸公式の前提知識が必要になるので、今回は、これらの知識を必要としない問題のみを解くことにする。
問題1 曲線y=x−sinx(0≦x≦2π)の概形をかけ。また、この結果を利用して、次の不等式を証明せよ。
y=x−sinxだから、
よって、0=f(0)≦f(x)≦f(2π)=2π。
最小値 0 (x=0)最大値 2π (x=2π)
凹凸表を書くと
x | 0 | … | π | … | 2π |
y'' | 0 | + | 0 | − | 0 |
凸凹 |
| 下に凸 | 変曲点 | 上に凸 |
|
よって、グラフは次の通り。
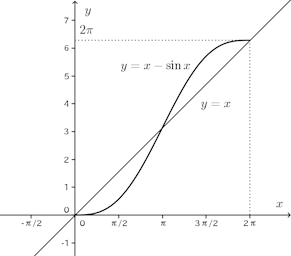
f(x)=x−sinx(0≦x≦π/2)とすると、f(x)は単調増加。
よって、
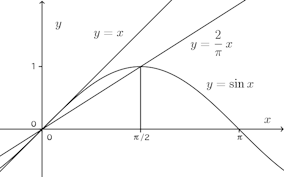
また、次のグラフをみれば、0<x<π/2で
問題2 次の問いに答えよ。
(1) 次の関数の極値を求め、グラフをかけ。
【解】
(1)
増減表を書くと、
x | 0 | … | π/4 | … | 5π/4 | … | 2π |
y' |
| + | 0 | − | 0 | + |
|
y | 0 | 増加 | 極大 | 減少 | 極小 | 増加 | 0 |
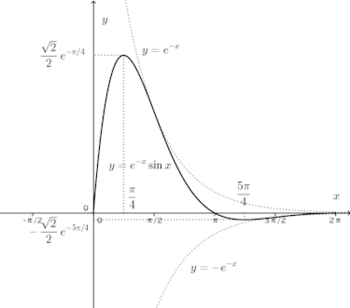
(2)
増減表を書くと、
x | 0 | … | π/3 | … | π |
y' |
| − | 0 | + |
|
y |
| 減少 | 極小 √3 | 増加 |
|
よって、x=π/3のとき最小で、最小値は√3。
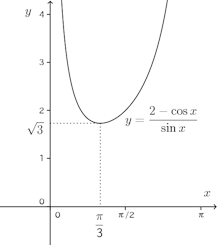
(解答終わり)