ワンポイントゼミ ちょっと嫌な問題

ワンポイントゼミ　ちょっと嫌な問題

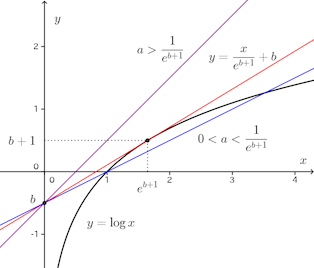
問題　方程式logx=ax+b（a>0）が実数解をもつための条件を求めよ。また、その時の点(a,b)の存在する範囲を図示せよ。

【解】

　　

とおく。

これはx>0で微分可能。

　　

a>0だから、f(x)はx=1/aのとき極大、かつ、最大。

極大（最大）値は

　　

よって、f(x)=0が実数解をもつ条件は

　　

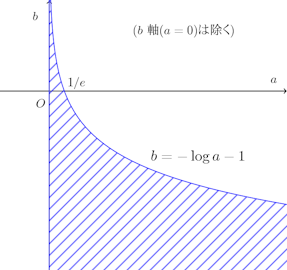
（解答終わり）

（※）

f(1/a)>0のとき、

　　

よって、中間値の定理より0と1/aと、1/aと∞の間にf(x)=0、つまり、logx=ax+bの解が存在する。

f(1/a)=0のとき、x=1/aが解である。

f(1/a)<0のとき、f(x)≦f(1/a)<0となり、f(x)=0をみたす実数解は存在しない。
このことは、次の図を見れば、明らかでしょう。

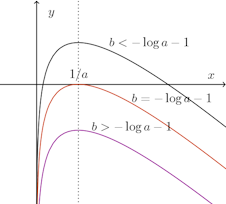
意欲のある人は、

y=logxとy=ax+b(a>0)の交点を調べることにより、この問題を解いて欲しい。

（ヒント：y=ax+bを点(0,b)を通る傾きaの直線と考える。そして、(0,b)からy=logxに引いた接線を求める。）

さらに意欲のある人は、

　　

とし、

y=aとの交点を調べることにより、この問題を解いて欲しい。

さらに意欲のある人は、a>0という条件を取り払って解く。

これでやめようと思ったのですが、とつだけ、別解を。

【別解】

(0,b)からy=logxに引いた接線を求める。

接点を(t,logt)とすると、接線の方程式は

　　

これが点(0,b)を通るので

　　

よって、接線の方程式は

　　

上図より明らかなように、y=ax+bの傾きが

　　

のとき、y=ax+bとy=logxは共有点をもつ。

a>0だから、両辺の対数をとると

　　

（別解おわり）

こちらの方がわかりやすくて、スッキリしているのかもしれない。

タグ：微分積分

ワンポイントゼミ 曲線外の点から指数関数、対数関数へ引いた接線の求め方

ワンポイントゼミ　曲線外の点から指数関数、対数関数へ引いた接線の求め方

曲線y=f(x)上の点(a,f(a))における、この曲線の接線の方程式は

　　

指数、対数関数の微分は

　　

したがって、指数関数、対数関数の点(a,f(a))における接線の方程式は、それぞれ

　　

となる。

 

問　原点O(0,0)からにひいた接線の方程式と接点の座標を求めよ。

【解】

接点のx座標をaとする。

上の点における接線の方程式は、

　　

これが原点O(0,0)を通過するので

　　

したがって、接点は(1,e)で、接線の方程式は

　　

また、y=logx上の点(a,loga)におけるこの曲線の接線の方程式は、

　　

これが原点を通過するので、

　　

したがって、接点は(e,1)で、接線の方程式は

　　

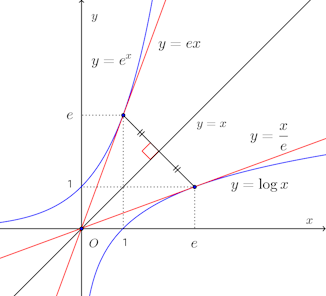
（解答終わり）

丁寧に書くと、解答はこのようになる。

ところで、対数関数y=logxは指数関数の逆関数であり、同様に、指数関数はy=logxの逆関数。

y=exのxとyを入れ換えて

　　

が、原点からy=logxへ引いた接線の方程式になっている。

図形の対称性を利用して、このように解くこともできるという、ただ、それだけの話です。

 

問題　方程式の実数解の個数を調べよ。

とy=mxとすると、問の結果より、とy=mxが接するのはm=eのとき。

ということで、次のグラフから

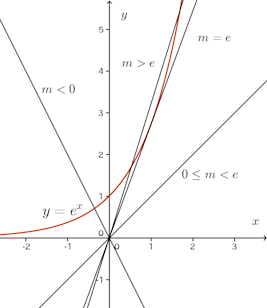
　　m<0のとき、解の個数１

　　0≦m<eのとき、解なし

　　m=eのとき、解の個数１

　　m>eのとき、解の個数２

ということになる。

こうした図を使った解答は厳密さに欠けるという批判はありますが・・・。

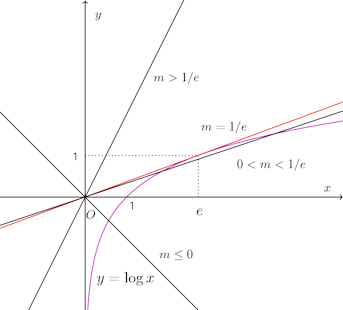
類題　方程式logx=mxの実数解の個数を調べよ。

原点を通る接線は既に求めてある。あとはy=logxの図をかけば出てくるんじゃないですかい？

タグ：微分積分

指数関数の微分と凹凸

指数関数の微分と凹凸

指数関数の微分は

　　

さらに

　　

では、問題を。

問題１　次の関数の凹凸を調べよ。

　　

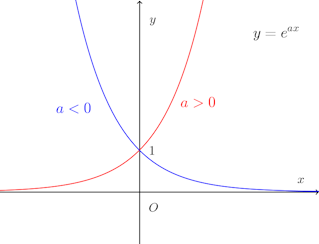
【解】

　　

a≠0だからa²>0。よって、f''(x)>0となり、f(x)は下に凸である。

（解答終わり）

問題２　次の関数のグラフの概形をかけ。

　　

【解】

（１）

　　

とおくと、

　　

したがって、x=−1で極小で極小値は

　　

f''(x)は

　　

凹凸表を書くと

x	…	−2	…
f''(x)	−	0	＋
f(x)	上に凸	変曲点（−2/e²）	下に凸

したがって、グラフは以下の通り。

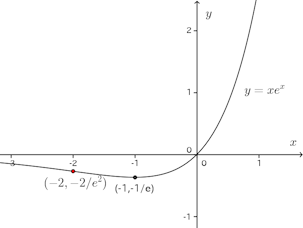
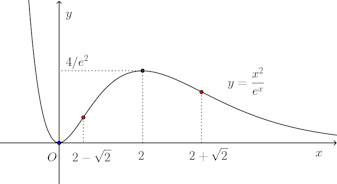
（２）

とおいて、
　　

増減表を書くと

x	…	0	…	2	…
f'(x)	−	0	＋	0	−
f(x)	減少	極小（0）	増加	極大（4/e²）	減少

２次導関数f''(x)は

　　

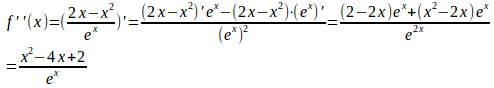
となる。

分母はつねに正なので、f''(x)の符号は分子であるx²−4x+2の符号と同じ。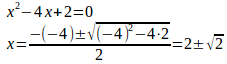
　　

したがって、凹凸表は次のようになる。

x	…	2−√2	…	2+√2	…
f''(x)	＋	0	−	0	＋
f(x)	下に凸	変曲点	上に凸	変曲点	下に凸

グラフは次の通り。

（解答終わり）

なのですが、これらのグラフを正確に書くためには

　　

が必要になる。

ということで、次の問題。

問題３　x>0のとき、次の不等式が成立することを証明せよ。

　　

【解】

n=1のとき、x>0で

　　

が成り立つことを証明する。

　　

とすると、x>0で

　　

したがって、f(x)はx>0で単調増加。

ゆえに、

　　

n=kのとき

　　

が成り立つと仮定する。

n=k+1のとき

　　

とし、xで微分すると

　　

①より

　　

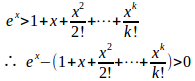
したがって、x>0でf'(x)>0となり、f(x)は単調増加。

よって、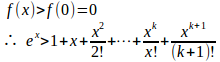
　　

となり、n=k+1のときも成立する。

以上のことより、数学的帰納法によって

　　

である。

（解答終了）

ということで、

x>1のとき、
　　

で、

　　

だから、ハサミ打ちの定理より、

　　

だから、問題２の（２）の

　　

はx→∞のとき、y→0である。

（１）の場合は、t=−xとおくと、x→−∞のときy→+∞になることを利用して

　　

このことから、x→−∞のときy→0になることが分かる。

さらに、t=logxとおくと

　　

さらに、x→∞のとき、t→+∞になることを利用して

　　

前回の極限を求めることができた。

タグ：微分積分