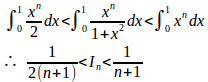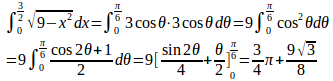ウイルス感染のデジタル家電が震源か 脆弱な「IoT」がハッカーの標的に 産経 [ネコ騙し数学]
ウイルス感染のデジタル家電が震源か 脆弱な「IoT」がハッカーの標的にhttps://t.co/EVuKKnXS0T #ダイン #米大規模サイバー攻撃
— 産経ニュース (@Sankei_news) 2016年10月23日
定積分の漸化式 [ネコ騙し数学]
定積分の漸化式
問題1
(1) I₁を計算せよ。
(2) 次の不等式を証明せよ。
【解】
(1)
(2) 0≦x≦1だから1≦1+x²≦2。
よって、
(3)
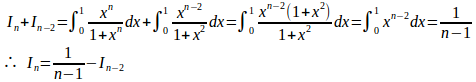
(解答終了)
少し説明すると、(1)の積分では
この場合、f(x)=1+x²とすると、f'(x)=2xになるので、
(2)では、a≦x≦bにおいて、f(x)≦g(x)ならば、恒等的にf(x)=g(x)でなければ
また、
問題2
【解】
とおくと、dx=-dθ。x=0のときθ=π/2、x=π/2のときθ=0。
とすると、
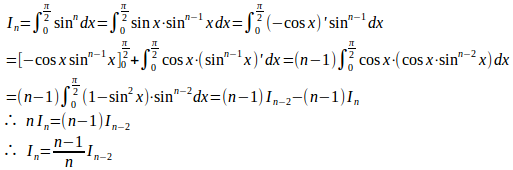
よって、nが偶数のとき
nが奇数のとき
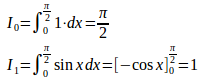
したがって、
nが偶数のとき
問題2の結果を用いると、
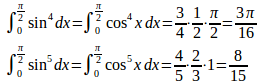
と簡単に計算することができる。
問題3
を求め、それを利用して、nが正の整数のときのを求めよ。
ここで、
したがって、
定積分の部分積分法 [ネコ騙し数学]
定積分の部分積分法
f(x)、g(x)が閉区間[a,b]で連続な導関数を有するものとすると
問題1 次の不定積分の値を求めよ。
(1)
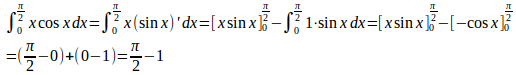
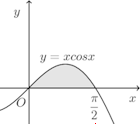
(2)
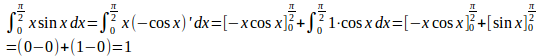
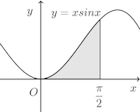
(3)
と考え、
(4)
問題2 次の定積分の値を求めよ。
(1)
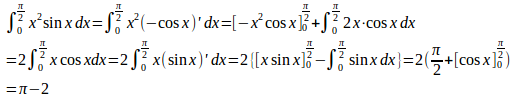
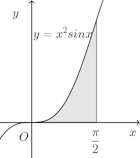
(2)
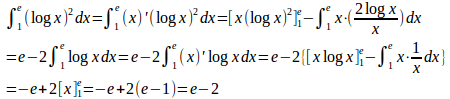
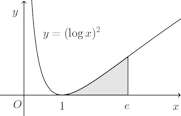
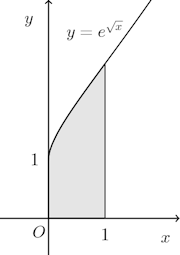 (3) √x=tとおくt、x=t²、dx=2tdt。また、x=0のときt=0、x=1のときt=1。
(3) √x=tとおくt、x=t²、dx=2tdt。また、x=0のときt=0、x=1のときt=1。
したがって、
この問題2のように、数回、部分積分をしたり、置換積分と部分積分を組み合わせて、定積分の値を求める場合がある。
問題3 次の定積分を求めよ。
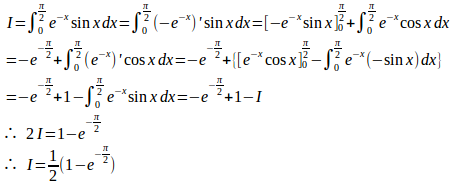
(解答終了)
そして、
定積分の置換積分法2 [ネコ騙し数学]
定積分の置換積分法2
問題1 次の公式が成り立つことを証明せよ。
f(x)=f(a−x)のときは
t=a−xとおくと、dt=−dx。
また、x=0のときt=a、x=aのときt=0。したがって、
次に、
f(a−x)=−f(x)ならば
(1)より
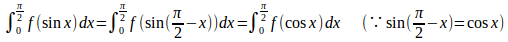
問題2
(1) 次の等式を証明せよ。(2) 次の定積分の値を求めよ。
(1)
したがって、
(2) (1)より
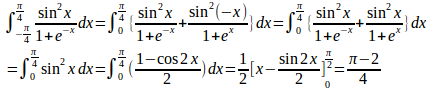
(解答終了)
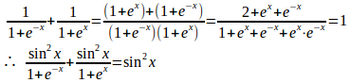
問題3
(1) f(x)が0≦x≦1で連続な関数のとき、次の等式を証明せよ。
(1) x=π−tとおくと、dx=−dt。x=0のときt=π、x=πのときt=0。
したがって、 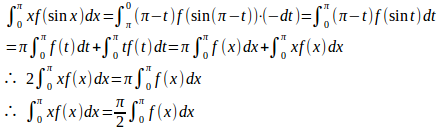
(2) (1)より
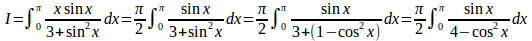
ここで、t=cosxとおくと、
したがって、
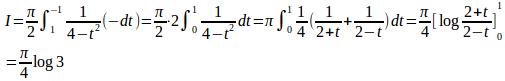
(解答終了)
問題4
次の□の中に文字、数を入れて、そのことを証明しなさい。
(1)
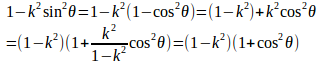
したがって、
このとき、
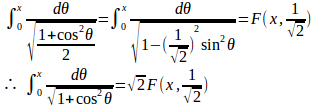
よって、□の中は1/√2、1/√2
(2) 1−k²sin²θのところが1−k²x²になっているんだから、x=sinθと置けというのでしょう。
x=0のときθ=0、x=1/2のときθ=π/6とすると、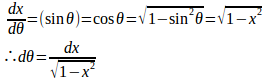
だから、
(解答終了)
ワンポイントゼミ 定積分の置換積分のグラフ [ネコ騙し数学]
ワンポイントゼミ 定積分の置換積分のグラフ
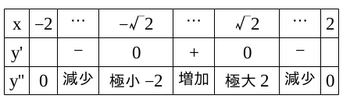
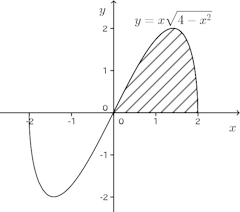
のグラフ
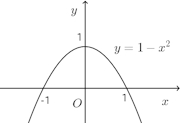 分母である1+x²>0だから、y'の符合は分子である1−x²と同じ。
分母である1+x²>0だから、y'の符合は分子である1−x²と同じ。
そして、x=±1でf'(x)=0。
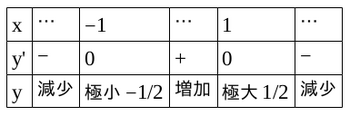
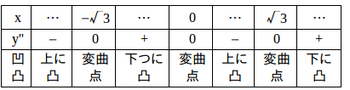
以上のことから、増減表は次のようになる。
また、
以上のことから、この関数のグラフは下図のようになる。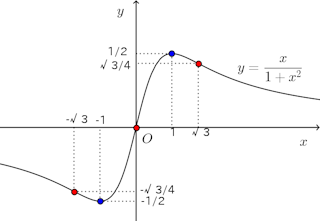
なお、ここで、青い点は極値、赤い点は変曲点をあらわしている。
なのですが、この関数は
つまり、この関数は原点に関して対称なので、この対称性を利用することも可能である。
のグラフ
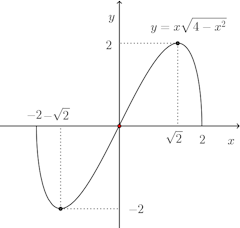 また、
また、
定積分の置換積分法 [ネコ騙し数学]
定積分の置換積分法
§0 イントロ
次の定積分を考える。
定積分の定義は、F(x)をf(x)の原始関数とすると、
したがって、①の定積分の値は
ここで、②に注目して欲しい。
x=1のとき、t=2、x=0のときt=1だから、わざわざ、②をxの関数に戻す必要はなく
さらに、遡って
つまり、t=x²+1とおくと
一般的に書くと、t=g(x)で、α=g(a)、β=g(b)のとき
§1 定積分の置換積分法
x=g(t)とおくとき、a=g(α)、b=g(β)で、g(t)がα、βを両端とする区間で連続な導関数をもつならば、
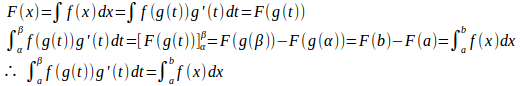
したがって、x=g(t)とおいたとき、
問題1 次の定積分の値を求めよ。
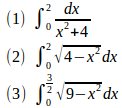
【解答】
(1) x=2tanθ(−π/2<θ<π/2)とおくと、x=0のときθ=0、x=2のとき、θ=π/4。また、
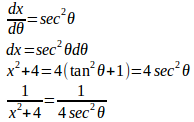
したがって、
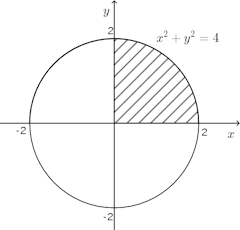
(2) x=2sinθ(−π/2≦θ≦π/2)とおくと、x=0のときθ=0、x=2のときθ=π/2。
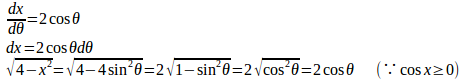
したがって、
(3) x=3sinθとおくと、x=0のときθ=0、x=3/2のとき、θ=π/6。
したがって、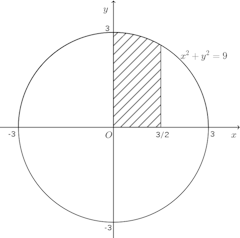
(解答終了)
問題2 次の定積分の値を求めよ。
(2) t=4−x²とおくと、x=0のときt=4、x=2のときt=0。
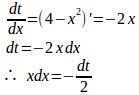
したがって、
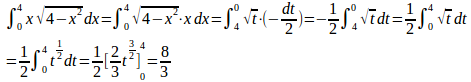
(2)は、x=2sinθとおいて
そして、cosθ=tとおくと、θ=0のときt=1、θ=π/2のときt=0。
定積分の計算2 三角関数 [ネコ騙し数学]
定積分の計算2 三角関数
三角関数を含む積分の計算には、以下に示す三角関数の公式が必要になることがある。
倍角公式
積和の公式
三角関数の合成公式
問題1 次の定積分の値を求めよ。
(1) 2倍角の公式より
(2) m=nのとき
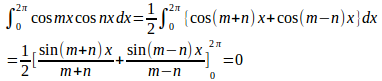
したがって、
(3)
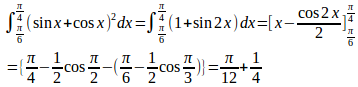
(解答終了)
(2)と同様の計算をすることによって、
結果をまとめると、
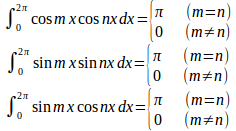
そして、このことから、次のことが言える。
問題2
【解】
lを正の整数とすると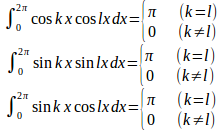
が成立する。
また、
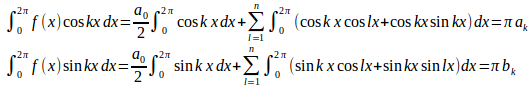
したがって、
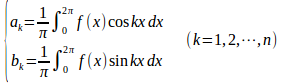
(解答終了)
問題では有限項であるが、これを無限級数に拡張したものがフーリエ級数である。
定積分の計算1 [ネコ騙し数学]
定積分の計算1
関数f(x)の原始関数をF(x)とするとき、関数f(x)のaからbへの定積分は
今回は、置換積分、部分積分法を用いずに求められる定積分の計算を中心に述べることにする。
問題1 次の定積分の値を求めよ。
(1) (x+1)(x²−1)=x³+x−x−1と展開して、定積分の計算を行なう。
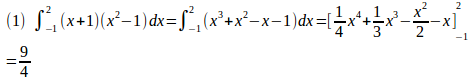
(2) この定積分は、
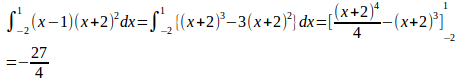 このようにすると、x=−2のとき、x+2=0になるので、計算の省力化がはかれ、計算間違いをする確率が低くなる。
このようにすると、x=−2のとき、x+2=0になるので、計算の省力化がはかれ、計算間違いをする確率が低くなる。(3) この定積分を求めるには、絶対値を外す必要がある。
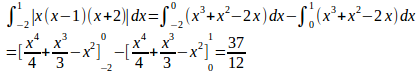
(解答終了)
ちなみに、
問題2 次の定積分の値を求めよ。
(1) x²+3x+1=(x+2)(x+1)−1だから
(2) これは、次のように部分分数に分けて、計算する。
したがって、
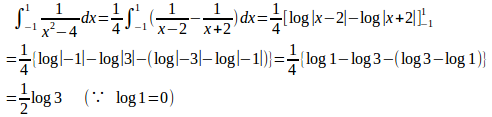
(3)
(2)の定積分は、
ここで1つ質問するが、
定積分(数学3) [ネコ騙し数学]
定積分(数学3)
§1 定積分の定義
関数f(x)は閉区間[a,b]で連続とする。この区間をn個の小区間に分け、その分割を
とし、その小区間にそれぞれ任意の点をとって、和
このとき、おのおのの小区間の幅を0に近づくようにnの値を限りなく大きくすると、区間の分け方、小区間の点のとり方にかかわらず、和は一定の極限値に近づく。
この極限値を、関数f(x)のaからbまでの定積分といい、記号
上の定義で、特に、分点を等間隔にとり、をその分点と一致するようにとると、
である。
また、閉区間[a,b]内の点cを分点の1つにとり、[a,b]を[a,c]と[c,b]に分ければ、
a<bとして定積分を定義したが、
a=bのとき
また、定積分の重要な性質として、次のものがある。
定理
a<b、かつ、[a,b]でつねにf(x)≦g(x)のとき、つねにf(x)=g(x)でないかぎり、
§2 積分の平均値の定理と定積分と不定積分との関係
積分の平均値の定理を証明する前に、中間値の定理と最大値・最小値の定理。
中間値の定理
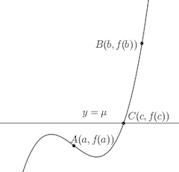
f(x)が有界閉区間[a,b]で連続で、f(a)≠f(b)であるならば、f(a)とf(b)の間のすべてのμに対して
最大値・最小値の定理
f(x)が有界閉区間I=[a,b]で連続ならば、f(x)はIで最大値と最小値をとる。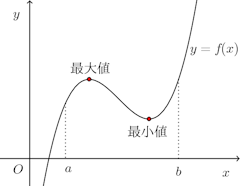
次に、積分の平均値の定理を紹介し、それを証明することにする。
積分の平均値の定理
関数f(x)が有界閉区間[a,b]において連続でならば、
【証明】
f(x)が定数関数であるとき、a<c<bであるすべてのcについて成立する。f(x)が定数でないとき、a≦x≦bにおけるf(x)の最小値m=f(x₁)、最大値M=f(x₂)とする。
m≦f(x)≦Mだから、a<bのとき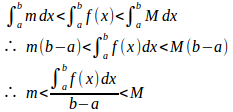
である。
よって、中間値の定理より、f(c)=μを満たすcがx₁とx₂の間に少なくとも1つ存在する。
したがって、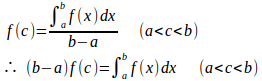
(証明終了)
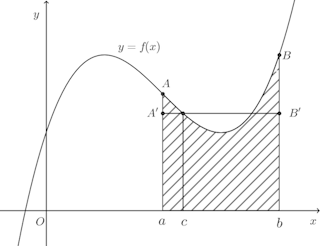
幾何的に言うならば、積分の平均値の定理は、図のように曲線y=f(x)とx=a,x=b、x軸で囲まれた図形(斜線部)と長方形A'abB'の面積を等しくするような直線A'B'が存在することを意味している。
定理
f(x)の原始関数の1つをF(x)とするとき
【証明】
h<0のとき
となるcが存在する。
いずれにせよ、
したがって、
問題 積分の平均値の定理を用いて
となるθが存在することを証明せよ。
【解】f(x)は閉区間[0,1]で連続で、積分の平均値の定理より
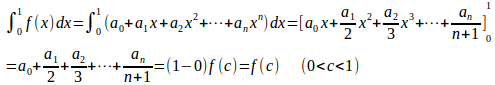
となるcが存在する。
g(x)=sinxは0≦θ≦π/2で連続、かつ、g(0)=0、g(π/2)=1だから、中間値の定理より、0<c<1に関して
したがって、
となるθが存在する。
(解答終了)微分方程式の応用2 [ネコ騙し数学]
微分方程式の応用2
問題1 曲線上の1点Pにおける法線がx軸と交わる点をN、Pからx軸におろした垂線の足をQとするとき、QNの長さを法線影という。法線影がつねに一定値aであるような曲線を求めよ。
【解】
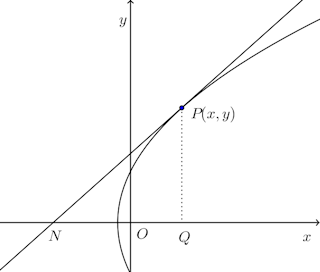 曲線上の点Pの座標を(x,y)とすると、点Pにおける曲線の接線の方程式の傾きは
曲線上の点Pの座標を(x,y)とすると、点Pにおける曲線の接線の方程式の傾きはである。したがって、点Pにおける法線の方程式は、
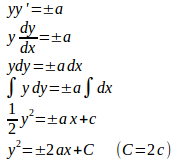
(解答終了)
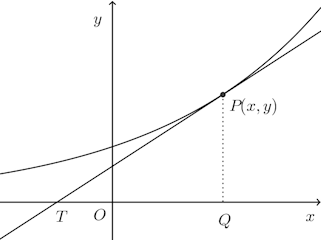
問題2 曲線上の1点Pにおける接線がx軸と交わる点をT、Pからx軸におろした垂線の足をQとするとき、QTの長さを接線影という。接線影がつねに一定の値aである曲線を求めよ。
【解】
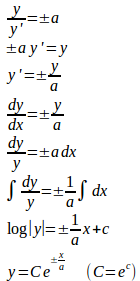
(解答終了)
正確に言うと関数方程式になるのだけれど、実質的に微分方程式なので次の微積分の総合問題を解くことにする。
問題 曲線y=f(x)(x≧0、y≧0)の上の動点Pからx軸、y軸に引いた垂線の足を、それぞれQ,Rとするとき、x軸、y軸、垂線PQ、曲線y=f(x)で囲まれた面積が、x軸、y軸,直線PR、直線x=1で囲まれた部分の面積よりもつねに2だけ小さいという。f(x)を求めよ。
ただし、f(x)はx≧0で微分可能とする。【解】
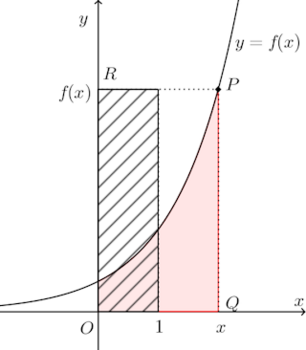 x軸、y軸、垂線PQ、曲線y=f(x)で囲まれた面積は薄いピンクで示された図形の面積で、この面積S₁は
x軸、y軸、垂線PQ、曲線y=f(x)で囲まれた面積は薄いピンクで示された図形の面積で、この面積S₁は
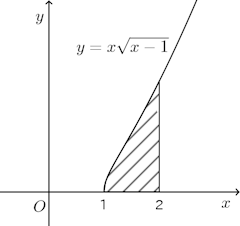
問題4 関数y=f(x)はx≧0で増加する連続関数で、x>0のときf(x)>0とする。また、この関数のグラフは点(1,2)を通る直線で、次の性質をもつ。
曲線上の任意の点を通ってx軸、y軸にそれぞれ平行な2つの直線を引くとき、この2直線とx軸、y軸で囲まれる長方形の中で、曲線の下側の部分の面積は残りの部分の面積の2倍である。この関数f(x)を求めよ。
【解】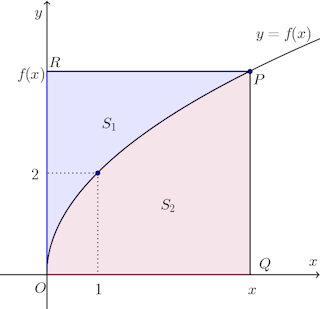 曲線上の点Pの座標を(x,f(x))とし、点Pをとおりx軸に平行な直線とy軸との交点をR、Pを通りy軸と平行な直線とx軸との交点をQとする。
曲線上の点Pの座標を(x,f(x))とし、点Pをとおりx軸に平行な直線とy軸との交点をR、Pを通りy軸と平行な直線とx軸との交点をQとする。
図に示すように、直線OR、直線RPと曲線y=f(x)で囲まれた図形の面積をS₁、直線OQ、直線QP、曲線y=f(x)で囲まれた図形の面積をS₂とする。
問題の条件より