微分方程式の応用２

微分方程式の応用２

 

問題１　曲線上の１点Pにおける法線がx軸と交わる点をN、Pからx軸におろした垂線の足をQとするとき、QNの長さを法線影という。法線影がつねに一定値aであるような曲線を求めよ。

【解】

曲線上の点Pの座標を(x,y)とすると、点Pにおける曲線の接線の方程式の傾きはである。したがって、点Pにおける法線の方程式は、

　　

法線とx軸と交わる点Nのx座標をXとすると、

　　

したがって、QNの長さは

　　

よって、
　　

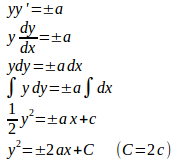
（解答終了）

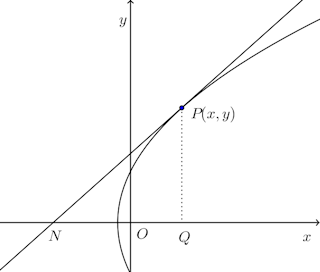
問題２　曲線上の１点Pにおける接線がx軸と交わる点をT、Pからx軸におろした垂線の足をQとするとき、QTの長さを接線影という。接線影がつねに一定の値aである曲線を求めよ。

【解】

曲線上の点Pの座標を(x,y)とすると、接線の方程式は

　　

よって、Tのx座標をXとすると、

　　

QTの長さは

　　

したがって、
　　

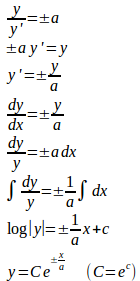
（解答終了）

正確に言うと関数方程式になるのだけれど、実質的に微分方程式なので次の微積分の総合問題を解くことにする。

問題　曲線y=f(x)（x≧0、y≧0）の上の動点Pからx軸、y軸に引いた垂線の足を、それぞれQ，Rとするとき、x軸、y軸、垂線PQ、曲線y=f(x)で囲まれた面積が、x軸、y軸,直線PR、直線x=1で囲まれた部分の面積よりもつねに２だけ小さいという。f(x)を求めよ。

ただし、f(x)はx≧0で微分可能とする。

【解】

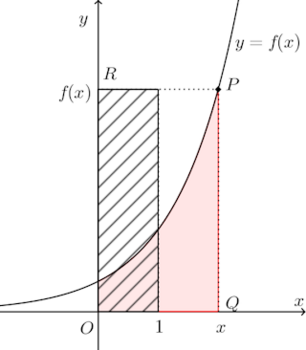x軸、y軸、垂線PQ、曲線y=f(x)で囲まれた面積は薄いピンクで示された図形の面積で、この面積S₁は

　　

x軸、y軸,直線PR、直線x=1で囲まれた部分の面積S₂は斜線部で示される図形の面積であり、

　　

問題の条件よりS₁=S₁−2だから

　　

両辺をxで微分すると

　　

y=0は解として不適だから、

　　

①より、x=0のとき

　　

したがって、

　　

よって、解は

　　

（解答終了）

問題４　関数y=f(x)はx≧0で増加する連続関数で、x>0のときf(x)>0とする。また、この関数のグラフは点(1,2)を通る直線で、次の性質をもつ。

曲線上の任意の点を通ってx軸、y軸にそれぞれ平行な２つの直線を引くとき、この２直線とx軸、y軸で囲まれる長方形の中で、曲線の下側の部分の面積は残りの部分の面積の２倍である。

この関数f(x)を求めよ。

【解】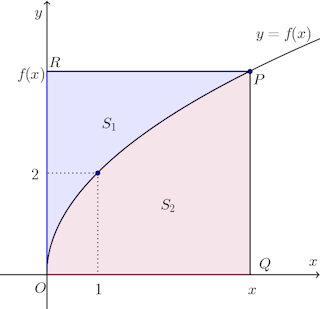

曲線上の点Pの座標を(x,f(x))とし、点Pをとおりx軸に平行な直線とy軸との交点をR、Pを通りy軸と平行な直線とx軸との交点をQとする。

図に示すように、直線OR、直線RPと曲線y=f(x)で囲まれた図形の面積をS₁、直線OQ、直線QP、曲線y=f(x)で囲まれた図形の面積をS₂とする。

問題の条件より

　　

長方形OQPRの面積はxf(x)だから、

　　

したがって、

　　

S₂は

　　

よって、

　　

両辺をxで微分すると、

　　

この微分方程式をとくと

　　

この曲線は(1,2)を通るので

　　

よって、

　　

（解答終了）

タグ：微分積分