積分を用いた不等式の証明

積分を用いた不等式の証明

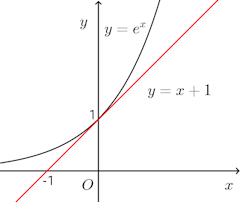
問題１　x>0のとき、次の不等式が成立することを証明せよ。

微分を使って証明するならば、たとえば、次のような証明になるだろう。

【証明】

　　

f(x)はx>0で微分可能。

そこで、f(x)の変化を調べるために、f(x)を微分すると

　　

したがって、f(x)はx≧0で単調増加。

よって、

　　

（証明終了）

また、とすると、

　　

したがって、y''>0で、この関数yは下つに凸。

また、x=0におけるこの曲線の接線の方程式は

　　

下に凸の関数の性質（曲線は接線の上側にある）より、x>0ならば

　　

である。

（右図参照）

この他にも、微分を用いた証明法はいくつかあるだろう。

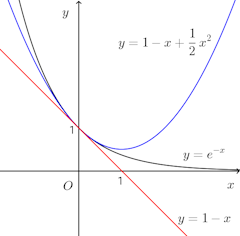
なのだけれど、積分を使うと、次のように簡単に証明できてしまう。

【積分を用いた証明】

　　

したがって、x>0ならば、

　　

（証明終わり）

実は、これだけでなくて、

　　

だから、x>0のとき

　　

同様に、順次計算することによって

　　

を証明することができる。

正確な証明をするならば、数学的帰納法を使って。

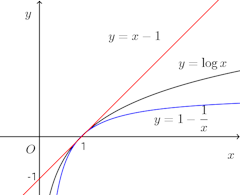
問題２　積分を使って次の不等式を証明せよ。

　　

【証明】

（１）　t>0ならば、

　　

したがって、x>0ならば

　　

t>0のとき

　　

だから、x>0のとき

　　

以上のことより、

x>0ならば

　　

（２）　x>1とすると、t∈(1,x)の任意のtに対して

　　

よって、
　　

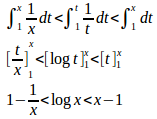
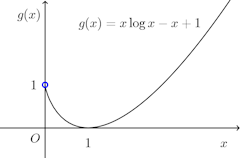
0<x<1とすると、t∈(x,1)の任意のtに対して

　　

よって、
　　

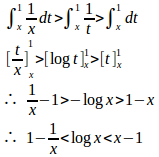
x=1のとき、

　　

となり、等号が成立。

よって、

　　

（証明終わり）

問題２の（２）より、x>0のとき

　　

この両辺にxをかけると

　　

これは、定積分と不等式１の問題３の（１）の不等式であり、積分を使ってこの不等式を証明したことになる。

また、（２）の不等式

　　

にxをかけると

　　

さらに

　　

したがって、ハサミ打ちの定理より

　　

である。

ワンポイントゼミ２２では、ロピタルの定理を使ってこの極限を求めたが、ロピタルの定理を使うことなくこの極限を求めることができた。

タグ：微分積分