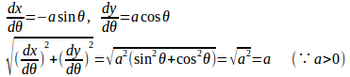積分の応用 曲線の長さ

積分の応用　曲線の長さ

§１　曲線の長さ

滑らかな曲線y=f(x)上の２点A(a,f(a))、B(b,f(b))の曲線の長さを考える。

下図のように[a,b]を

　　

とn個に等分割し、

　　

とする。

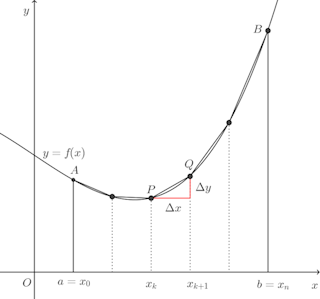
このとき、弧PQの長さl(PQ)は線分PQの長さ

　　

で近似される。

平均値の定理より
　　

よって、

　　

したがって、曲線上の点A、Bの曲線の長さl(AB)は

　　

で近似され、

　　

になる。

すなわち、

曲線y=f(x)（a≦x≦b）の長さLは

　　

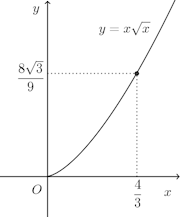
問題１　次の曲線のこの長さを求めよ。

　　

【解】

（１）

　　

曲線の長さをLとすると
　　

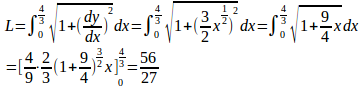
（２）

　　

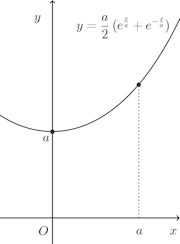したがって、曲線の長さをLとすると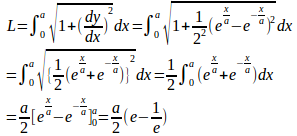
　　

（解答終了）

§２　媒介変数で表された曲線の長さ

媒介変数tで表された曲線

　　

の区間α≦t≦βに対応する弧の長さをLとする。

α≦t≦βにおいてf'(t)>0の場合、

　　

だから、
　　

よって、媒介変数でx=f(t)、y=g(t)（α≦t≦β）で表された曲線の曲線の長さLは

である。

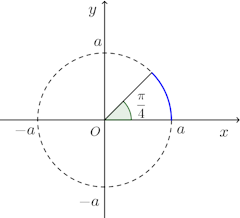
問題２　媒介変数で表された次の曲線の弧の長さを求めよ。

【解】

（１）
　　

よって、

　　

（２）　　　　

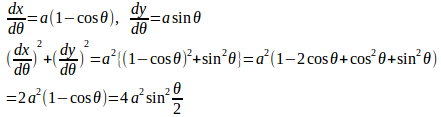
よって

　　

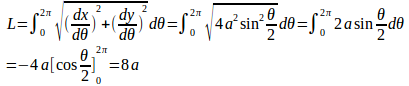
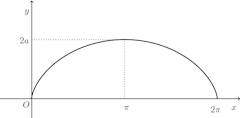
（３）

　　

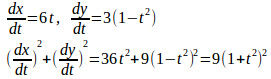
よって

　　

（解答終了）

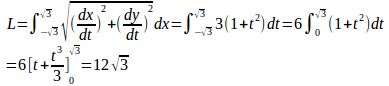
台形公式と中点公式とによる定積分の近似計算

台形公式と中点公式とによる定積分の近似計算

定積分

　　

の近似計算法として台形公式とシンプソンの公式を紹介した。

その最も基礎となるのが、

　　

という２つの式。

（１）が台形公式で、（２）がシンプソンの公式。

（１）と（２）が幾何的に何をあらわしているか明らかにするために、

a≦x≦bにおいてy=f(x)>0という曲線を考える。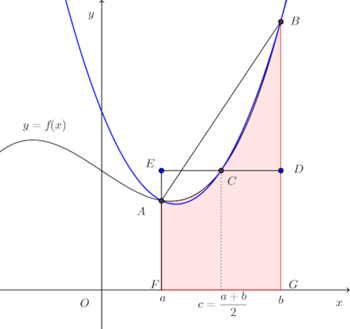

そして、A(a,f(a))、B(b,f(b))、F(a,0)、G(b,0)とする。

そうすると、

　　

は、y=f(x)とx軸、さらにx=a、x=bとで囲まれた面積に等しい。

（１）は台形ABGFの面積に等しい。何故ならば、

　　

となるからだ。

さらに、線分FGの中点のx座標をcとすると、

　　

になる。

そして、

　　

とし、A、B、Cの３点を通る放物線をg(x)（図中の青い曲線）とすると、

　　

になる。

つまり、（２）は曲線y=f(x)を放物線で近似し、その面積を求めて①で定まる面積Sを近似している。

台形公式はy=f(x)を直線で近似、シンプソンの公式では放物線で近似しているのだから、一般論として、（１）より（２）の方がより真実の面積Sに近い値を示す。

これはあくまで一般論だケロよ。

では、ここで質問する。

点a、点bの中点cにおけるf(c)を高さとする四角形DEFGの面積、すなわち、

　　

と、台形公式(1)、シンプソンの公式、そして、あらたに登場した（３）の中点公式、どちらが精度よくSを計算できるだろうか？

あくまで一般論として、中点公式（３）がシンプソンの公式に勝つことはないだろう。

だとすれば、

中点公式と台形公式の勝負だケロ。

簡単なf(x)=x²

　　

で試してみると、台形公式だと

　　

中点公式だと

　　

だから、

　　

つまり、台形公式（１）よりも中点公式(2)の方が精度よく計算できている。
上の例だと、台形公式は中点公式よりも誤差が２倍も大きい。裏を返せば、中点公式は台形公式よりも２倍精度がよい。

　　

台形公式だと変わらずS₁=1/2。

中点公式だと

　　

したがって、

　　

が成立している。

この２という数字は偶然だろうか・・・。

ちなみに、シンプソンの公式はf(x)が３次関数までは正確な値を出す。
　　

シンプソンの公式で計算してみると、

　　

２次関数で近似しているのに、３次関数まで正確な値を出す。

不思議だと思わないかい。

閉区間[a,b]をn個の区間に分割し、この区間に対して台形公式と中点公式を適用し定積分を近似すると、

　　

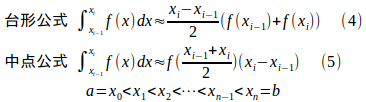
等間隔に分割されている場合、

　　

だから、

　　

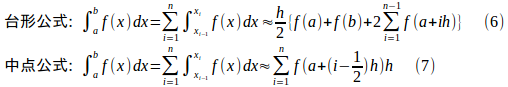
台形公式と中点公式で定積分の近似計算をするプログラムをBloggerの方にアップしておいた。

　　中点公式と台形公式の精度比較
　　　http://nemneko.blogspot.jp/2016/11/blog-post_14.html

プログラムのデフォルト設定は

　　

[0,1]の分割数nを増やすとどうなるか、この計算の場合、どちらのほうが精度がいいのかを確かめて欲しい。

ちなみに、n=10のときの計算結果は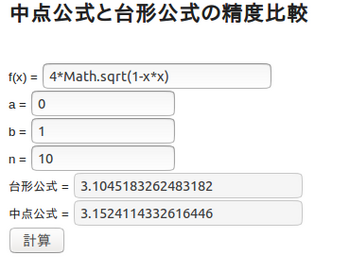

（イメージです。だから、計算ボタンをクリックしても何も起きない）

n=100のときの計算結果は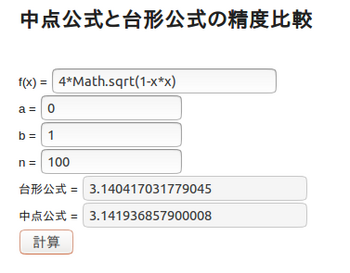

（イメージです！！）

台形公式よりも中点公式のほうが精度よく計算できていることが分かるのではないか。

タグ：微分積分

定積分の応用 体積の最大最小に関する問題

定積分の応用　体積の最大最小に関する問題

問題１　点(1,1)を通るだ円

　　

をx軸のまわりに回転してできる回転体の体積の最小値を求めよ。

【解】

　　

したがって、回転体の体積Vは

　　

また、

　　

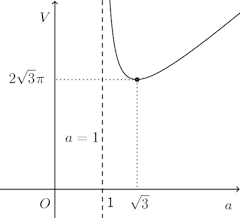が点(1,1)を通るので

　　

b²>0から、a>1。

②を①に代入すると、

　　

これをaで微分すると、

　　

したがって、a=√3のとき最小で、最小値は、2√3π

（解答終了）

問題２

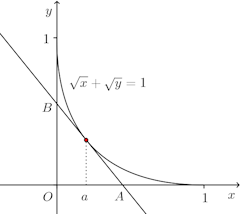
（１）　曲線

　　

上のx座標がa（0<a<1）である接線の方程式を求めよ。

（２）　上の接線とx軸、y軸とで囲まれる図形を、x軸のまわりに回転してできる立体の体積を最大にするaを求めよ。

【解】

（１）

　　

したがって、

　　

よって、x座標がaである曲線上の点に接線の方程式は

　　

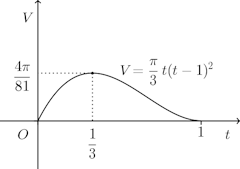（２）　上の接線とx軸、y軸との交点をA、Bとすると、AとBの座標は、それぞれ、√a,0)、(0,1−√a)。

そして、求める体積Vは△OABをx軸わまりに回転してできる円錐に等しいので

　　

ここで、t=√aとおくと

　　

これをtで微分すると、

　　

したがって、t=1/3、すなわち、a=1/9のときに最小になる。

（解答終了）

問題３　２つの曲線

　　

のx軸に垂直な共通弦をABとする。ABと曲線②で囲まれた図形をx軸のまわりに回転してできる回転体について、次の問いに答えよ。

（１）　この回転体の体積をaであらわせ。

（２）　aがいろいろな値をとって変わるとき、この立体の体積の最大値を求めよ。

【解】

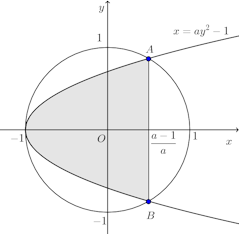（１）　曲線①と曲線②の交点を求める。②より

　　

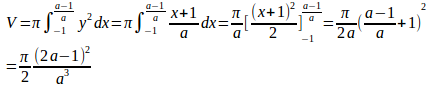
これを①に代入しy²を消去すると、

　　

a>1/2だから

　　

よって、求めるべき体積Vは
　　

（２）

　　

だから

　　

とおき、この関数の増減を調べることにする。

f(a)をaで微分すると、

　　

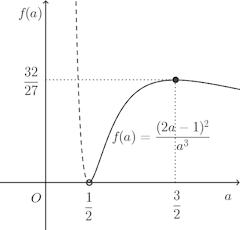この増減表を書くと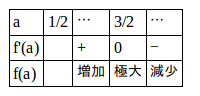

よって、f(a)はa=3/2のとき、最大。

したがって、Vはa=3/2のときに最大で、最大値は

　　

（解答終了）

 

タグ：微分積分

２次精度のルンゲ＝クッタ法もなかなか侮れない

２次精度のルンゲ＝クッタ法もなかなか侮れない

２次精度のルンゲ＝クッタ法のプログラムにミスを発見し――修正オイラー法に引きずられて勘違いした(^^ゞ――、プログラムを修正するのと同時に、２次のルンゲ＝クッタ法を使って２階の常微分方程式の初期値問題を解くことのできるプログラムをC言語で作ってみた。

そのついでに、

　　

を解かせてみた。

この微分方程式は、単振動、たとえば、バネの運動をあらわす微分方程式で、上の初期条件で解くと、解は次のようになる。

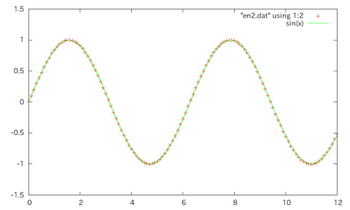
２次精度のルンゲ＝クッタ法を用いて、xの増分をh=0.1という数値計算としては、かなり粗い計算を120ステップ計算させてみた。

これがその結果。

文句なしの精度で正弦関数を再現出来ていることがわかると思う。

しかも、驚くなかれ、物理でいうところのエネルギー保存則もほとんど満たしている。

　　

とおくと、①の微分方程式は

　　

と変形できる。

この微分方程式は、変数分離法を使って、

　　

左辺第１項は物理でいうところの運動エネルギー、そして、左辺第２項はバネの弾性エネルギーに相当する。

そして、上の式は、運動ネルギーとバネの弾性エネルギーの和は一定で変化しないことをあらわしている。

つまり、力学的なエネルギーは不変、保存されるということだにゃ。

初期条件、つまり、x=0のとき、y=0、y'=u=1だから、（２）より、

　　

そして、これから

　　

次のように考えることもできる。

　　

さてさて、解いた答えがこの関係を満たしているかどうかだにゃ。

下の図は、２次精度のルンゲ＝クッタ法で解いたものを、縦軸にu、横軸にyをとって表したもの。

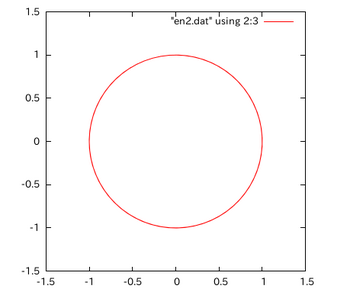
計算結果はほとんど円を描いている。

つまり、エネルギーはほとんど保存されている。

数値計算だと、計算を進めるとu²+y²の値は次第次第に増加し、120ステップだから約２周でu²+y²≒1.003まで増加するけれども、分割の幅h=0.1という粗い計算であることを考えると、良好な計算結果と言っていいのだろう。

もっとひどい結果、悲劇的な結果が出ると思っていたので、正直、意外であった。

（修正）オイラー法、ルンゲ＝クッタ法で（１）の２階微分方程式を解くには、

　　

と、１階の連立微分方程式に変換して解く。

この方法については、いずれ、きちんと紹介するにゃ。

実は、４次精度のルンゲ＝クッタを用いて２階の常微分方程式の初期値問題を解くBASICのブログラムは１年以上前に紹介しているのだけれど、あのときには理論的な話を一切しなかったので、そういった話をすこし含めて話すつもりでいるにゃ。

あくまで予定だにゃ。

そのための準備を少しずつしている。

C言語で申し訳ないけれど、計算に使ったプログラムは次の通り。

（１）以外の問題でも解けるように、汎用性を持たせてある。

　　

を

　　

と変換して解かせている。

 

#include <stdio.h>

#include <math.h>

doublef(double x,double y,double p) {

return -y;

}

double g(double p) {

return p;

}

void RungeKutta2(double x, double y, double p, double h, int n) {

double k11, k12, k21, k22;

int i;

printf("%f %f %f %f \n",x,y,p,y*y+p*p);

for (i = 1 ; i <= n; i++) {

k11= h*g(p);

k21= h*f(x,y,p);

k12= h*g(p+k21/2);

k22= h*f(x+h/2,y+k11/2,p+k21/2);

x=x+h;

y=y+k12;

p=p+k22;

printf("%f %f %f %f \n", x,y,p,y*y+p*p);

}

}

main() {

double x,y,h,p;

int n;

n=120;

h=0.1;

x=0;y=0;p=1;

RungeKutta2(x,y,p,h,n);

}

ちなみに、このプログラムでいじっていいのは、

doublef(double x,double y,double p) {

return -y;

}

の黄色の部分と、

main() {

double x,y,h,p;

int n;

n=120;

h=0.1;

x=0;y=0;p=1;

RungeKutta2(x,y,p,h,n);

}

の黄色の部分だけです。

間違っても、ルンゲ＝クッタ法の計算の本体だけはいじらないでください。

ここをいじると、大変な事になるので注意してください。

タグ：微分積分

積分の応用 体積４ パラメータ（媒介変数）で表された図形の体積

積分の応用　体積４　パラメータ（媒介変数）で表された図形の体積

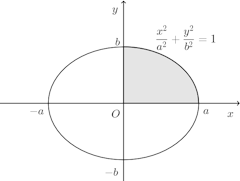
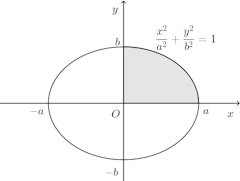問題１　だ円x=acosθ、y=bsinθによって囲まれた部分をx軸のまわりに回転して得られる立体の体積を求めよ。ただし、a、bは正の実数とする。

【考え方】

x=acosθ、y=bsinθから媒介変数θを消去し
　　

このだ円はy軸に関して対称だから、体積Vは

　　

と簡単に解くことができる。

しかし、問題１のように媒介変数（パラメータ）を消去して曲線の方程式が求められるとは限らないし、求められたとしても、それが複雑な形で計算に困る場合がある。

そこで、媒介変数を消去するのではなく、置換積分を用いて媒介変数のまま計算し、体積を求めることにする。

体積は

　　

x=acosθ、y=bcosθだから、被積分関数であるy²は

　　

x=0、x=aにはθ=π/2、θ=0が対応し、

　　

したがって、

　　

この式中の
　　

だから、

　　

（考え方終了）

 

問題２　次の図形をx軸のまわりに回転してできる立体の体積を求めよ。

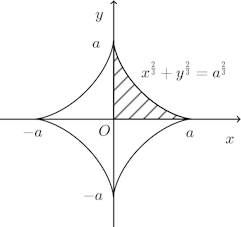
（１）　曲線（アステロイド）

　　

の囲む部分。

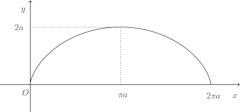
（２）　曲線（サイクロイド）

　　

とx軸で囲まれる部分。

【解】
（１）　この図形はy軸に関して対称だから、求める体積Vは第１象限の部分をx軸のまわりに回転して得られる立体の体積の２倍である。

したがって、

　　

x=0、x=aはθ=π/2、θ=0に対応し、

　　

したがって、

　　

（２）　x=0、x=2πaにはθ=0、θ=2πが対応し、

　　

したがって、体積Vは
　　

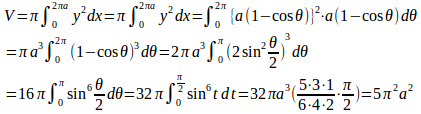
（解答終了）

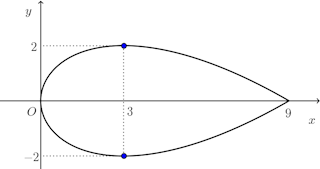
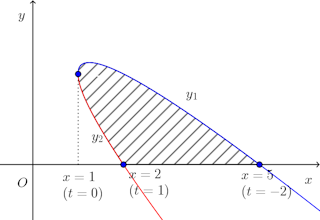
問題３　x=1+t²、y=2−t−t²で表される曲線とx軸とで囲まれる図形がx軸のまわりに回転してできる立体の図形の体積を求めよ。

【解】

この曲線がx軸とまじわる点ではy=0だから

　　

したがって、x軸との交点は(1、0)、(5,0)。

この図形は右図のとおり。

この曲線の上側（青い曲線）をy₁、下側（赤い曲線）をy₂とおくと、

体積はVは

　　

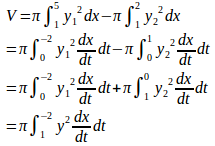
dx/dt=2tだから

　　

（解答終了）

 

問題３の解答が理解できない人は、

　　

として、

　　

を計算すればよい。

タグ：微分積分

定積分の応用 体積３

定積分の応用　体積３

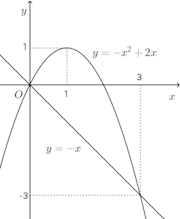問題１　曲線y=−x²+2xと直線y=−xとで囲まれた部分をx軸のまわりに回転してできる回転体の体積を求めよ。

この問題のように、２曲線が回転軸に関して同じ側にない場合、回転した際の曲線の上下で重なる部分の様子がわかりづらい。

このような場合、曲線、直線に絶対値をつけたもので考えるとよい。つまり、

　　

そうすると、次の図になる。

【解】

回転の元になる図をx軸の上側にくるようにx軸で折り返して考えると、

外側の線は

　　

内側の線は

　　

したがって、

　　

（解答終了）

 

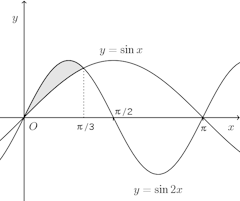
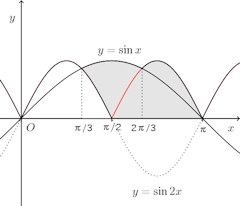
問題２　２つの曲線y=sinx、y=sin2xで囲まれた次の部分をx軸のまわりに回転してできる立体の体積を求めよ。

（１）　0≦x≦π/3の範囲で囲まれた部分

（２）　π/3≦x≦πの範囲で囲まれた図形

【解】

（１）



体積Vは

　　

（２）　曲線y=sin2xの3/π≦x≦πの部分をx軸に関して対称に折り返して考えると、下の図のようになる。

したがって、体積Vは

　　

（解答終了）

タグ：微分積分

定積分の応用 体積２

定積分の応用　体積２

２曲線で囲まれた部分をx軸まわりに回転して得られる図形の体積

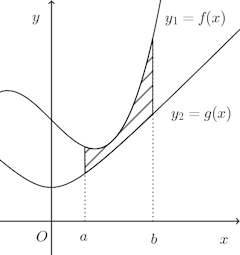閉区間[a,b]（a≦x≦b）において、２つの曲線y₁=f(x)とy₂=g(x)がx軸の同じ側にあって、｜f(x)｜≧｜g(x)｜とすると、この２曲線とx=a、x=bで囲まれた部分をx軸まわりに回転して中空の回転体の体積Vは

　　

である。

つまり、

　　V=（外側にできる体積）−（内側にできる体積）

である。

問１　次の図形をx軸のまわりに回転して得られる図形の体積を求めよ。

（１）　曲線y=√xと直線y=xとで囲まれた図形

（２）　曲線y=cosx（−π/3≦x≦π/3）と直線y=1/2とで囲まれた図形

【解】

（１）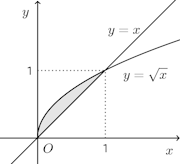



y=√xと直線y=xとの交点のx座標はx=0、x=1。

また、0≦x≦1において、x≦√xだから

　　

（２）

　　

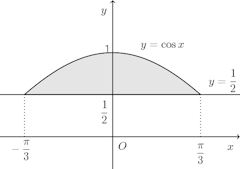
（解答終了）

問２　次の図形をy軸のまわりに回転して得られる図形の体積を求めよ。

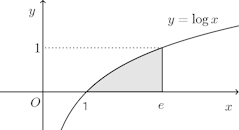
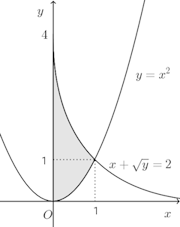
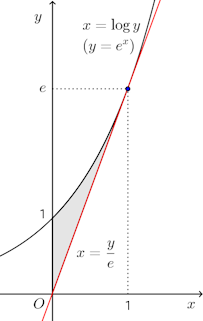
（１）　曲線y=logxと２直線y=e、x軸で囲まれた図形

（２）　２つの曲線y=x²、x+√y=2とy軸で囲まれた図形

【解】

（１）


　y=logxをxについて解くと

　　

x=eとy=logxの交点のy座標は1だから体積Vは

　　

（２）　２つの曲線y=x²、x+√y=2の交点のy座標は

　　

また、、x+√y=2のy切片は4。

したがって、

　　

（解答終了）

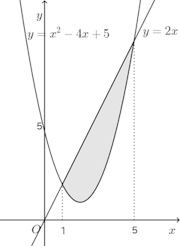
問題１　放物線y=x²−4x+5とy=2xで囲まれた図形をSとする。

（１）　Sをx軸のまわりに１回転してできる立体の体積を求めよ。

（２）　Sをy軸のまわりに１回転してできる立体の体積を求めよ。

【解】

（１）　y=x²−4x+5とy=2xの交点のx座標は

　　

したがって、体積は

　　

（２）　y=x²−4x+5をxについて解くと

　　

それで、

　　

とすると、求める体積は
　　

（解答終了）

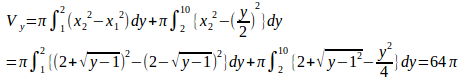
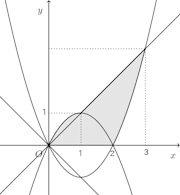
問題２　曲線と、原点からこの曲線に引いた接線とy軸とで囲む図形をy軸のまわりに回転してできる立体の体積を求めよ。

【解】

曲線上の点における接線の方程式は

　　

これが原点を通過するので、

　　

したがって、接線の方程式は

　　

よって、
　　

（解答終了）

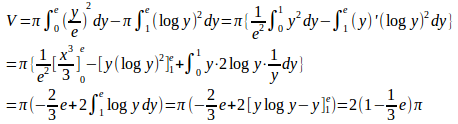
外側にできる立体の体積は

　　

内側にできる立体の体積は

　　

タグ：微分積分

定積分の応用 立体の体積

定積分の応用　立体の体積

§１　立体の体積

（１）　回転体の体積

曲線y=f(x)（a≦x≦b）をx軸のまわりに回転した体積を、x=g(y)（α≦y≦β）をy軸のまわりに回転した体積をとすると、

　　

である。

（２）　一般の立体の体積

座標xにおけて軸に垂直な切断面の面積がS(x)ならば、この立体のa≦x≦bの間の体積Vは

　　

§２　問題編

問題１　次の問いに答えよ。

（１）　y=1+√x、y=0、x=0、x=2の囲む部分をx軸のまわりに回転して得られる立体の体積を求めよ。

（２）　y=sinxとx軸とx=0およびx=πの囲む部分をx軸のまわりに観点して得られる立体の体積を求めよ。

（３）　曲線y=logxとx軸およびx=eで囲まれる部分をx軸のまわりに回転して得られる立体の体積を求めよ。

【解】

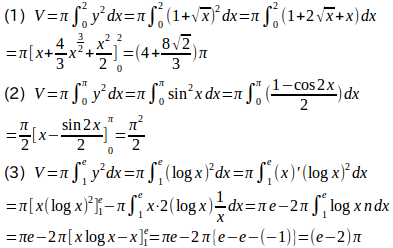
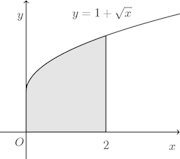
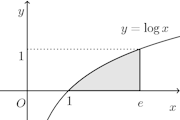
（解答終了）

問題２　次の問いに答えよ。

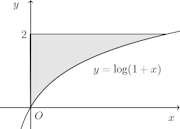
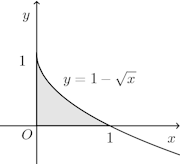
（１）　y=log(1+x)、y=2、y軸で囲まれた部分を、y軸のまわりに回転して得られる立体の体積を求めよ。

（２）　y=1−√xと両軸の世の部分で囲まれた部分をy軸のまわりに回転して得られる立体の体積を求めよ。

【解】

（１）　y=log(1+x)をxについて解くと

　　

よって、体積Vは

　　

（２）　y=1−√xをxについて解くと

　　

よって、

　　

（解答終了）

 

問題３　y=2sinxとy=1（π/6≦x≦5/6π)の囲む部分をy=1のまわりに回転して得られる立体の体積を求めよ。

【解】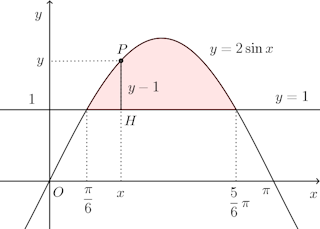

曲線y=2sinx上の動点Pの座標を(x,y)とし、Pからy=1に下ろした垂線の足をHとする。

y=2sinxをy=1まわりに回転させて得られる図形を、xで垂直に切った断面積S(x)は、PH=y−1だから

　　

したがって、この図形の体積Vは

　　

（解答終了）

 

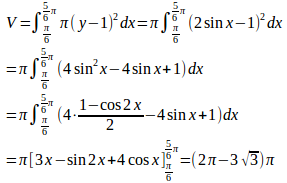
問題４　曲線y=cosx（−π/2≦x≦π/2）とx軸とで囲まれた図形が、x軸のまわりに回転してできる立体の体積V₁を求めよ。また、この図形をy軸ののまわりに回転してできる立体の体積V₂を求めよ。

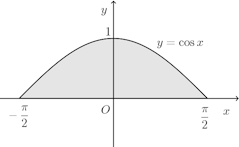【解】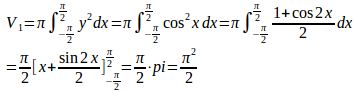　　
　　
y軸のまわりに回転して得られる体積V₂は

　　

y=cosxだから、y=0にはx=π/2、y=1には0が対応する。

したがって、

　　

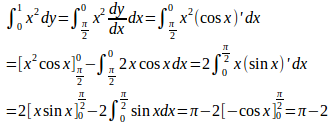
よって、

　　

（解答終了）

定積分 面積のラスト問題

定積分　面積のラスト問題

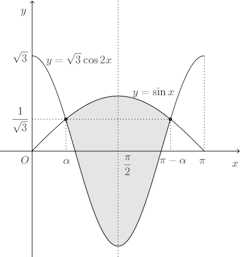
問題１　y=√3cos2x、y=sinxの２曲線（0<x<π）で囲まれた部分の面積を求めよ。

【解】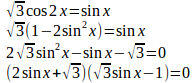

y=√3cos2x、y=sinxの交点のx座標は

　　

0<x<πではsinx>0だから、

　　

0<x<π/2の解をαとすると、解はαとπ−α。

すなわち、

　　

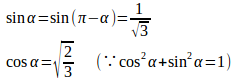
よって、面積Sは

　　

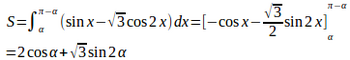
倍角公式より

　　

よって、

　　

（解答終了）

この図形はx=π/2に関して対称なので、対称性を利用して

　　

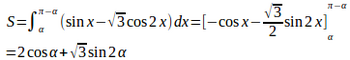
として、面積を求めた方が、厄介な三角関数の角関係を使わなくてすむので、計算が楽。

問題２　0≦x≦πの範囲における関数y=sinxのグラフをCとし、x軸と曲線Cとで囲まれる面積をAとする。Cをx軸に平行にa（a>0）だけ平行移動した曲線によって図形Aを２等分したい。aの値を求めよ。

【解】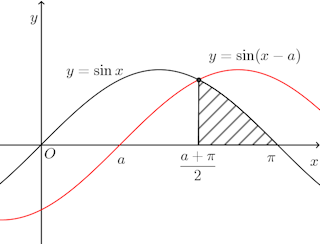

　　

y=sinxをx軸に平行にaだけ平行移動した曲線の方程式はy=sin(x−a)。

0<x<πにおいて、y=sinxとy=sin(x−a)の交点のx座標は

　　

問題の条件より、上図の斜線部は、A/4=1/2に等しいので、
　　

（解答終了）

y=sinxとy=sin(x−a)の交点のx座標は、たとえば、次のように求めることができる。

　　

問題の条件で上の方程式を満たす解は

　　

問題３

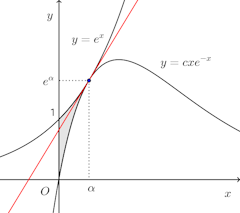
２つの曲線ととが点で共通の接線をもつとする。ただし、cは0でない定数とする。

（１）　c、αの値を求めよ。

（２）　この共通接線y=f(x)とするとき、0≦x<αでであることを示せ。

（３）　２曲線、および、y軸で囲まれ部分の面積を求めよ。

【解】

（１）

　　

x=αで共通接線ももつので

　　

①と②より

　　

この結果を①に代入すると

　　

（２）

　　

0≦x<1/2でy''<0。

よって、0≦x<1/2では上に凸。

したがって、
　　

（３） 　は下に凸だから、

　　

したがって、面積Sは

　　

ここで
　　

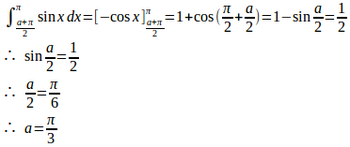
よって、

　　

（解答終了）

ちなみに、のグラフの概形は以下のとおり。

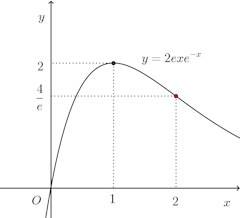
（２）より、この曲線は、x=1のときに極大で、x=2で変曲点をもつ。

 

問題４　関数

　　

のグラフとx軸とによって囲まれた各部分の面積の総和を求めよ。

【解】

のグラフはx軸とx=nπ（n=1,2,3,・・・）の点と交わる。

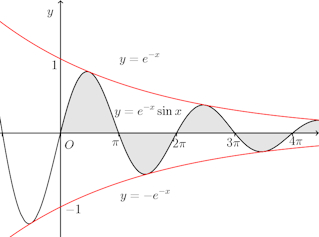
したがって、面積の総和は

　　

ここで

　　

とすると
　　

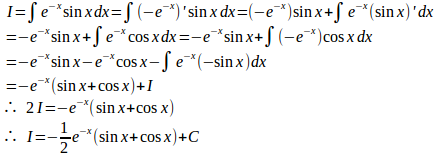
したがって

　　

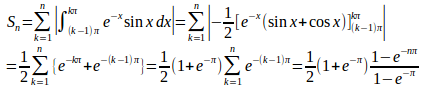
よって、

　　

（解答終了）

タグ：微分積分

定積分の応用 面積の最大・最小

定積分の応用　面積の最大・最小

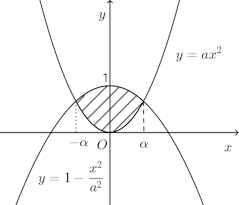
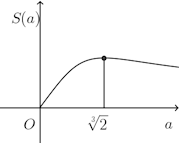
問題１　aを正の定数とし、y=ax²とによって囲まれる部分の面積をS(a)とするとき、S(a)を最大にするaの値を求めよ。

【解】

y=ax²ととの交点のx座標は

　　

ここで、

　　

とおくと、

　　

面積S(a)は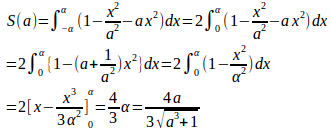
　　

S(a)の変化を調べるために、S(a)をaで微分すると、

　　

よって、のときに極大かつ最大。

（解答終了）

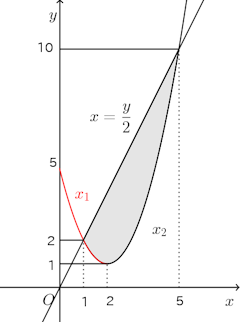
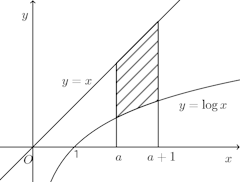
問題２　曲線y=logxと、３つの直線y=x、x=a、x=a+1（a>0）とで囲まれる部分の面積をSとする。

（１）　Sをaであらわせ。

（２）　Sを最小とするaの値を求めよ。

【解】

（１）

　　

（２）　Sをaで微分すると、

　　

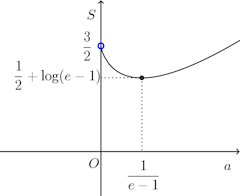よって

すなわち、のとき

すなわち、のとき

以上のことから、のとき、極小かつ最小で、最小値は

　　

（解答終了）

極小の判定は

　　

を使ってもいい。

こちらの方がわかりやすいのではないか。

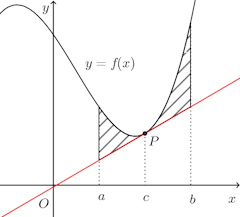
問題３　関数f(x)（a≦x≦b）が正の第２次導関数をもつとき、曲線y=f(x)上に点Pをとって、Pにおける接線とこの曲線とこの曲線x=a、y=bで囲まれた部分の面積を最小にするには、点Pをどのようにとればいいか。

【解】

接点Pの座標を(t,f(t))とすると、接線の方程式は

　　

よって、この接線とy=f(x)、x=a、x=bとで囲まれる部分の面積Sは
　　
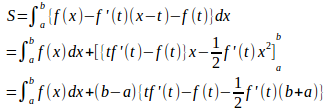
第１項は定数、またb−a>0だから、

　　

が最小のとき、Sは最小になる。

g(t)の変化を調べるために、g(t)をtで微分すると、

　　

a≦x≦bにおいてf''(t)>0だから、の前後でg'(t)の符合が負から正に変わる。

したがって、のときg(t)、Sともに最小になる。

よって、点Pを

　　

にとればよい。

（解答終了）

タグ：微分積分