定積分の応用 面積２

定積分の応用　面積２

問題１　次の図形の面積を求めよ。

（１）　曲線のx軸より下の部分とx軸とで囲まれた図形

（２）　0≦x≦2πの範囲で、２曲線y=sinxとy=sin2xとで囲まれた部分

【解】

（１）　y=cosx(1+sinx)とx軸との交点のx座標はπ/2と3π/2。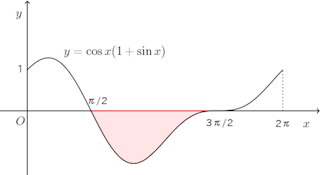

よって、求める面積Sは

　　

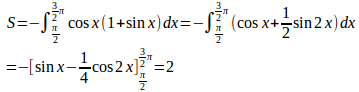
（２）　y=sinxとy=sin2xの交点のx座標は

　　

0≦x≦2πで、sinx=0になるのは、x=0、π、2π、cosx=1/2になるのはx=π/3、5π/3。
そして、この図形は点(π,0)に関して対称。

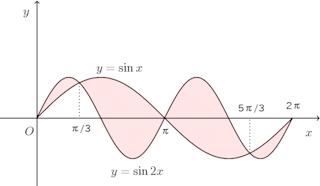
したがって、求める面積は

　　

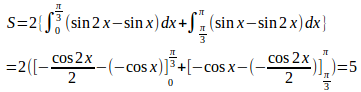
（解答終了）

問題２　次の図形の面積を求めよ。

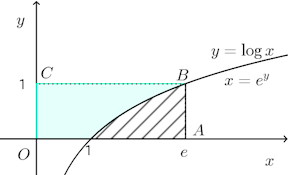
（１）　曲線y=logxとx軸、y軸および直線y=1で囲まれた部分。

（２）　曲線と直線y=xとで囲まれた部分。

【解】

（１）　y=logxだから、。

よって、求める面積Sは

　　

（別解）

求める面積は、□OABCから斜線部（x軸とy=logx、x=eで囲まれた部分）の面積を引いたものに等しいから

　　

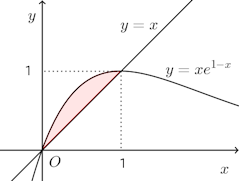
（２）　曲線と直線y=xとの交点のx座標は

　　

したがって、面積Sは

　　

ここで、
　　

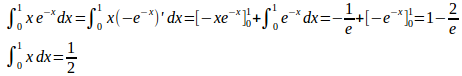
よって、

　　

（解答終了）

問題３　次の図形の面積を求めよ。

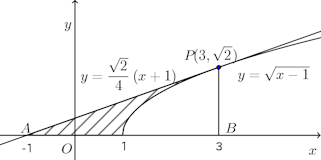
（１）　曲線と、点(3、√2)におけるこの曲線の接線およびx軸とで囲まれた部分

（２）　曲線y=logxと、この曲線の原点を通る接線およびx軸とで囲まれた部分

【解】

（１）　とすると

　　

したがって、接点P(3,√2)における接線の方程式は

　　

この接線とx軸との交点をAとすると、点Aのx座標は−1。

接点Pからx軸におろした垂線の足をBとすると、この図形の面積Sは

　　

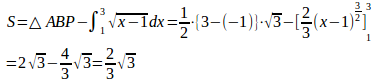
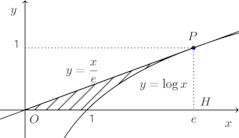（２）　接点Pの座標を(t,logt)とすると、接線の方程式は

　　

これが原点を通るので

　　

したがって、接線の方程式はy=x/e。

　　

よって、求める面積は

　　

（解答終了）

この問題３の（２）は、（１）同様に

　　

と求めることもできる。

問題４　y=ax²のグラフがy=logxのグラフと接するように定数aの値を定めよ。また、そのとき、これらのグラフとx軸とで囲まれる図形の面積を求めよ。

【解】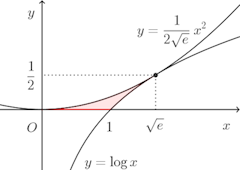

y=f(x)=ax²とy=g(x)=logxとの接点のx座標をtとすると、f(t)=g(t)、f'(t)=g'(t)。

　　

②よりat²=1/2。これを①に代入すると

　　

よって、

　　

したがって、面積Sは
　　

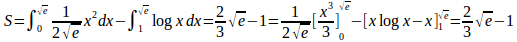
（解答終わり）

タグ：微分積分