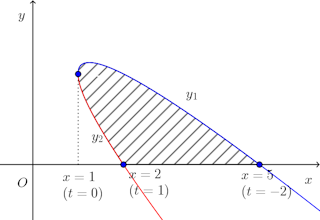
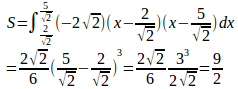ワンポイントゼミ x=t²+1、y=2−t−t²のグラフならび・・・

ワンポイントゼミ　x=t²+1、y=2−t−t²のグラフならび・・・

定積分の応用　面積４で出てきた次の方程式

　　

から

　　

とし、tを消去すると

　　

したがって、方程式x=t²+1、y=2−t−t²で与えられる曲線は、次の２つの曲線からなると考えることができる。

　　

よって、この曲線とx軸で囲まれる面積Sは

　　

t=x−1とおくと、

　　

また、

　　

両辺を２乗すると

　　

と、一つの方程式でこの曲線をあらわすことができる。

ここから先は読むな！！

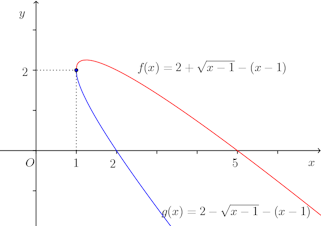
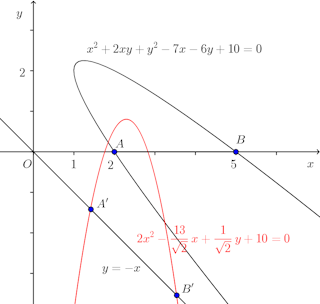この曲線の正体は、原点を中心に４５°時計回りに回転させるとわかります。

１次変換の知識を使い、

　　

として、これを①に代入すると、

　　

となり、この曲線の正体が放物線であることがわかる。

このとき、x軸はy=−xに写されるので、放物線

　　

と直線y=−xで囲まれた面積と等しいことになる。

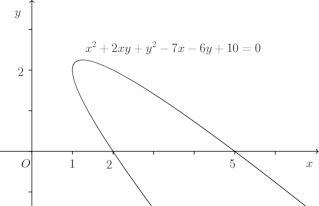
点A(2,0)、点B(5,0)の像A'、B'のx座標はそれぞれ2/√2、5/√2になるので、

放物線の定積分に関する次の公式

　　

を用いると、

　　

と求められる。

ちなみに、点(x,y)を原点を中心に半時計回りにθ回転して得られる点(x',y')は、行列を用いて書くと

　　

で、

　　

この場合、反時計回りに45°だから

　　

これから、A(2,0)、B(5,0)の像A'、B'のx座標は2/√2、5/√2となることが分かる。

あなた、読むなと言ったのに、読みましたね。




頭が呪われたにゃ！！

タグ：微分積分

定積分の応用 面積４ 媒介変数で表された曲線の場合２

定積分の応用　面積４　媒介変数で表された曲線の場合２

前回に引き続き、媒介変数で表された曲線の面積を求める問題を解くことにする。

前回解いた問題は、どれも、a≦x≦bにおいてdx/dt≧0、または、dx/dt≦0、つまり、xがtに関して（広義の）単調増加、または、単調減少の場合で、今回はより複雑なdx/dtの符合が正から負、または、負から正に変わるより複雑なものを扱うことにする。

 

問題１　曲線x=3t−t³、y=4−t⁴（−√2≦t≦√2）とx軸で囲まれた部分の面積を求めよ。

【解き方】

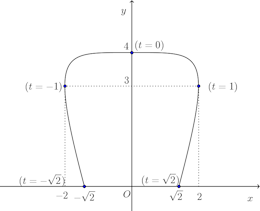この曲線とx軸との交点のtの値は、y=0から

　　

したがって、t=±√2。

　　

xはtの奇関数、yはtの偶関数だから、この曲線はy軸に関して対称（右図参照）。

したがって、求めるべき面積は第１象限の部分（0≧t≦√2）の面積の２倍である。

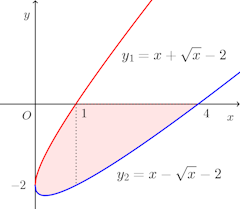
そこで、この曲線の0≦t≦1の部分をy₁、この曲線の1≦t≦√2の部分をy₂とおくと、右の図になる。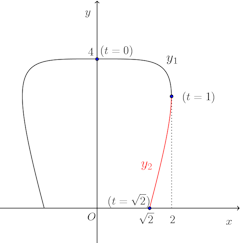

だから、曲線y₁、y₂、そして、x軸、y軸で囲まれた部分の面積は

　　

よって、求めるべき面積Sは

　　

【解き方終わり】

注意すべことは、0≦t≦√2のとき

　　

だから、0≦t<1ではxは増加、そして、1<t≦√2ではxは減少するということ。

そして、x=√2に対応するtはt=√2、x=2に対応するtはt=1であること。

だから、

　　

になっている！！
また、

　　

として、極値やyのxに対する増減を求めることができ、t=0のときにyは極大になることが分かる。

さらに、①をxで微分すると

　　

として、この曲線の凹凸を調べることもできる。

意欲のある人は、

　　

として、計算を続け、凹凸を調べて欲しい。

問題２　次の方程式のあらわす曲線とx軸とで囲まれた部分の面積を求めよ。

　　

上の問題は、x=t²からt=±√xとして、

　　

そして、

　　

とし、この２つの曲線の概形（右図参照）を書き、x軸との交点などを求める。

そして、

　　

と求めたほうが楽なのでしょうが・・・。

【解】

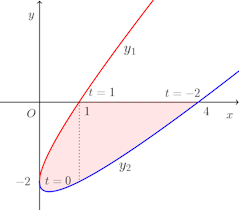y=t²+t−2とx軸との交点のtの値を

　　

−2≦t≦1で、xの取りうる値の範囲は0≦x≦4。

　　

−2≦t<0でxは減少し、t=−2のときx=4で、t=0のときx=0。

0<t≦1でxは増加し、t=0のときx=0、t=1のときx=1。

0≦t≦1の曲線の部分をy₁、−2≦t≦0の曲線をy₂とすると、

したがって、面積Sは

　　

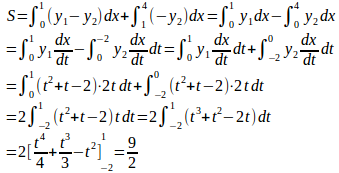
（解答終了）

問題３　tがすべての実数の範囲を動くとき、

　　

を座標とする点(x,y)は１つの曲線をえがく。この曲線とx軸とで囲まれる部分の面積を求めよ。

【略解】

　　

（略解終了）

なお、問題１、２、３では、

　　

という定積分の性質を使っている。

タグ：微分積分