定積分の応用 面積の最大・最小

定積分の応用　面積の最大・最小

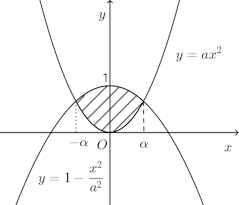
問題１　aを正の定数とし、y=ax²とによって囲まれる部分の面積をS(a)とするとき、S(a)を最大にするaの値を求めよ。

【解】

y=ax²ととの交点のx座標は

　　

ここで、

　　

とおくと、

　　

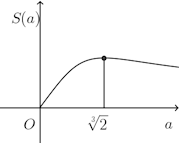面積S(a)は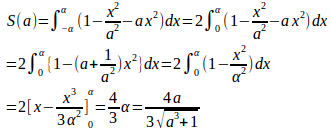
　　

S(a)の変化を調べるために、S(a)をaで微分すると、

　　

よって、のときに極大かつ最大。

（解答終了）

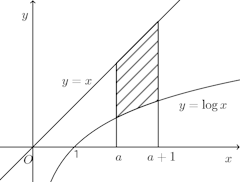
問題２　曲線y=logxと、３つの直線y=x、x=a、x=a+1（a>0）とで囲まれる部分の面積をSとする。

（１）　Sをaであらわせ。

（２）　Sを最小とするaの値を求めよ。

【解】

（１）

　　

（２）　Sをaで微分すると、

　　

よって

すなわち、のとき

すなわち、のとき

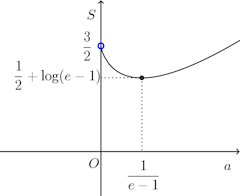
以上のことから、のとき、極小かつ最小で、最小値は

　　

（解答終了）

極小の判定は

　　

を使ってもいい。

こちらの方がわかりやすいのではないか。

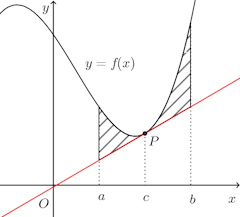
問題３　関数f(x)（a≦x≦b）が正の第２次導関数をもつとき、曲線y=f(x)上に点Pをとって、Pにおける接線とこの曲線とこの曲線x=a、y=bで囲まれた部分の面積を最小にするには、点Pをどのようにとればいいか。

【解】

接点Pの座標を(t,f(t))とすると、接線の方程式は

　　

よって、この接線とy=f(x)、x=a、x=bとで囲まれる部分の面積Sは
　　
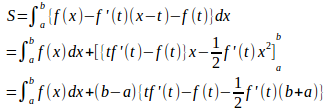
第１項は定数、またb−a>0だから、

　　

が最小のとき、Sは最小になる。

g(t)の変化を調べるために、g(t)をtで微分すると、

　　

a≦x≦bにおいてf''(t)>0だから、の前後でg'(t)の符合が負から正に変わる。

したがって、のときg(t)、Sともに最小になる。

よって、点Pを

　　

にとればよい。

（解答終了）

タグ：微分積分