定積分の応用 体積3 [ネコ騙し数学]
定積分の応用 体積3
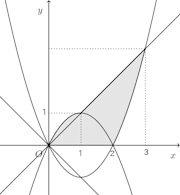
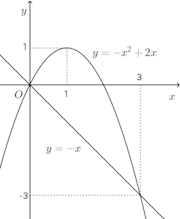 問題1 曲線y=−x²+2xと直線y=−xとで囲まれた部分をx軸のまわりに回転してできる回転体の体積を求めよ。
問題1 曲線y=−x²+2xと直線y=−xとで囲まれた部分をx軸のまわりに回転してできる回転体の体積を求めよ。
この問題のように、2曲線が回転軸に関して同じ側にない場合、回転した際の曲線の上下で重なる部分の様子がわかりづらい。
このような場合、曲線、直線に絶対値をつけたもので考えるとよい。つまり、
回転の元になる図をx軸の上側にくるようにx軸で折り返して考えると、
外側の線は
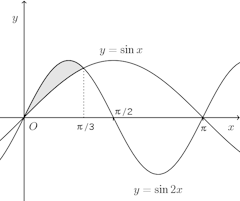
問題2 2つの曲線y=sinx、y=sin2xで囲まれた次の部分をx軸のまわりに回転してできる立体の体積を求めよ。
(1) 0≦x≦π/3の範囲で囲まれた部分(2) π/3≦x≦πの範囲で囲まれた図形
【解】
(2) 曲線y=sin2xの3/π≦x≦πの部分をx軸に関して対称に折り返して考えると、下の図のようになる。
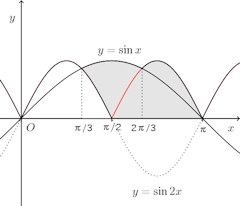
したがって、体積Vは
タグ:微分積分