定積分の応用 曲線の長さ2 [ネコ騙し数学]
定積分の応用 曲線の長さ2
【解】
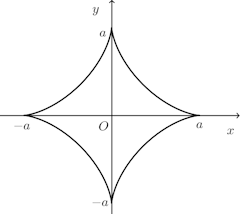
この曲線は
この図形は、x軸、y軸に関して対称だから、第一象限の曲線の長さを4倍したものが曲線の全長に等しい。
陰関数の微分法を用いた別解を紹介する。
【別解】
問題2 半径aの固定した糸を巻きつけておき、その端を円周上の一点Aから糸がたるまないようにほぐしていく。いま、円の中心Oを原点として、∠AOQ=θとするとき、
(1) 点Pの座標(x,y)をθを媒介変数としてあらわせ。(2) 点Pのえがく曲線(円の伸開線・インボリュート)の0≦θ≦2πの間の曲線の長さを求めよ。
【解】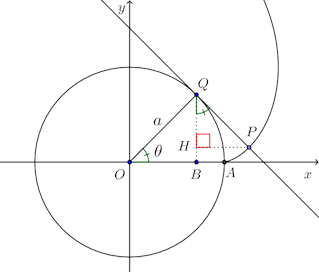 (1) Qからx軸におろした垂線の足をB、Pから直線BQにおろした垂線の足をHとする。
(1) Qからx軸におろした垂線の足をB、Pから直線BQにおろした垂線の足をHとする。
したがって、
(2)