定積分と関数列の極限 [ネコ騙し数学]
定積分と関数列の極限
定積分と関数列(の極限)の問題を解く前に、その準備として、漸化式で与えられる数列の極限の問題を解くことにする。
問 次のように定められた数列の一般項と極限を求めよ。
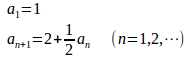
【解き方】
まず、
したがって、数列は初項a₁−4=−3、公比1/2の等比数列。
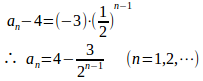
したがって、
方程式①の解α=4が極限値になっている。
これは偶然ではない。数列の極限値をαとすると、nが十分に大きいとき
はαに非常に近い値になるから、
これを漸化式に代入すると、
だが、次の漸化式で定められる数列の場合、
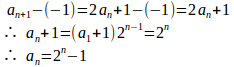
だから、この数列は発散し、有限確定な極限値は存在しない。
この手法で求められたαはあくまで極限値の候補に過ぎないことに注意して欲しい。
問題1
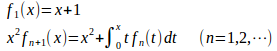
を求めよ。
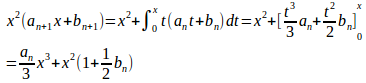
係数を比較すると、
よって、数列は公比1/2、初項b₁−2=−1の等比数列。
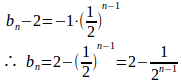
したがって、
問題にはないけれど、
つまり、関数の列は2に収束する。
問題2
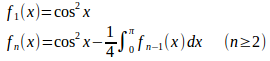
【解】
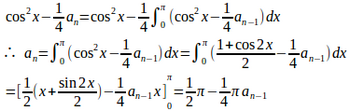
つまり
両辺からをひくと
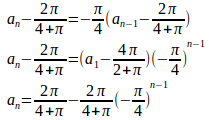
よって
(解答終了)
0<π/4<1だから、n→∞のとき
問題3 任意の実数aをとり、無限数列を次のように定める。
(1) x₀=a(2) が決まったとき、微分方程式
の解で、t=0のときを満たすものをy(t)とし、
とする。
を求めよ。
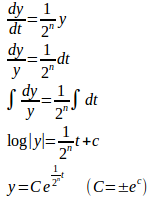
t=0のときだから
また、だから、上式にt=1を代入し
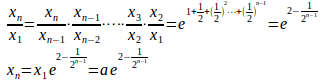
したがって、n→∞
タグ:微分積分



